Calculul dobanzii bancare

Calculul dobanzii bancare

In afara de inalta, moderata si redusa, dobanda la creditul bancar mai poate fi:

- dobanda simpla, adica pretul platit de imprumutat pentru suma de bani imprumutata pe timpul imprumutului:

- dobanda compusa, adica pretul platit de imprumutat pentru suma de bani reprezentand capitalul plus dobanda capitalizata pe o perioada anumita;

- dobanda fixa, care este valabila pe intreaga perioada a imprumutului;

- dobanda variabila, care se recalculeaza periodic in functie de evolutia dobanzii pe piata;

- dobanda negativa, care se percepe depunatorului pentru serviciile primite;

- dobanda preferentiala, perceputa pentru creditele acordate celor mai solvabili clienti;

- dobanda legala, nivelul maxim al ratei dobanzii permis de lege;

- dobanda camatareasca, dobanda situata peste pragul dobanzii legale;

- dobanda real pozitiva, dobanda care ia in considerare nivelul inflatiei.

1. Calculul dobanzii pentru creditul acordat statului prin cumpararea de titluri de catre banci priveste, pe de o parte, determinarea ratei scontului la care se emit titlurile, iar pe de alta parte determinarea ratei dobanzii la care se valorifica capitalul investit de cumparatorul de titluri de stat (banci sau alti investitori).

Rata scontului titlurilor de stat se obtine cu formula:

F - P 360

R_t = --- x ---

F n

unde:

Rt = rata dobanzii titlurilor de stat;

F = valoarea nominala a titlului;

P = pretul la care se vand titlurile;

n = numarul de zile pana la scadenta.

Rata dobanzii la care se valorifica capitalul investit de cumparatorii de titluri de stat (randamentul cuponului) se determina cu formula:

F - P 365

R_c = --- x ---

P n

2. Calculul dobanzii, atunci cand cel imprumutat (banca, in cazul depozitelor, si clientii acesteia, in cazul creditelor) primeste valoarea nominala a creditului si rambursarea, la scadenta, se face apeland la formula dobanzii simple:

P . r . t

D = ----

360

unde:

D = marimea absoluta a dobanzii; :

P = soldul capitalului (principalului);

r = rata anuala a dobanzii exprimata sub forma de coeficient;

t = perioada de acordare a imprumutului exprimata in zile.

In acest caz, calculul dobanzii se efectueaza o singura data la finele duratei de capitalizare (in cazul depozitelor) sau la scadenta )in cazul creditelor), utilizand o singura rata a dobanzii pentru perioada precizata de timp.

Din formula dobanzii simple se pot determina si ceilalti factori ai formulei: suma imprumutatului, rata dobanzii si perioada de creditare.

3. Rate ale dobanzii proportionale si echivalente

Fie o perioada de referinta (sa zicem anul) luata pentru unitatea de timp, si fie z durata unei alte perioade T (z este, in special, un numar rational). Spunem ca r si r_z sunt ratele dobanzii pentru perioade de referinta si, respectiv, pentru perioada T.

Fie V1 valoarea datorata pentru un capital C₀ pe perioada t si capitalizata la o rata r pe perioada de referinta; si fie V_z valoarea datorata pentru acelasi capital pe perioada cu aceeasi durata, t, si capitalizat la rata dobanzii r_z pe perioada T.

Spunem ca r_z si r sunt ratele dobanzii corespondente daca, si numai daca, valorile datorate V1 si Vz sunt egale oricare ar fi datele C₀ si t.

Primul caz - Capitalizarea la rate simple ale dobanzii

Prin definitie,

V₀ = C₀( 1 + r · t )

si

Egalitatea valorilor datorate este asigurata daca, si numai daca, exista relatia

r_z = z · r

Cazul al doilea - Capitalizarea la rate compuse ale dobanzii

Plecand de la relatia:

V₁ = C₀ ( 1 + r )^t

Egalitatea lui V1 cu Vz este asigurata daca:

V_z = C₀ (1+ r_z)^z =C₀[(1 + r_z)^z]^t

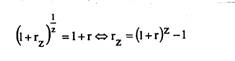
Se spune ca aceasta valoare r_z este echivalenta lui r.

4. Compararea ratei dobanzii proportionale cu rata dobanzii echivalente

a) daca 0<z<1, rata dobanzii proportionale este mai mare decat rata dobanzii echivalente.

b) daca z>1, rata dobanzii proportiona1e este mai mica decat rata dobanzii echivalente.

5. Rata efectiva a dobanzii si rata nominala a dobanzii (aparenta)

Rata efectiva a dobanzii ajusteaza rata nominala in functie de frecventa folosita pentru compunere si numarul de zile presupuse a fi intr-un an (360 sau 365 de zile). Ea este data de formula:

unde:

Ref = rata anuala efectiva a dobanzii;

r = rata anuala nominala a dobanzii;

m = numarul intervalelor (perioadelor) de compunere dintr-un an.

Rata efectiva este intotdeauna mai mare decat rata nominala (aparenta) a dobanzii

6. Rata reala a dobanzii si rata nominala a dobanzii

Datorita efectului inflatiei, puterea de cumparare a unei sume investite la o rata nominala a dobanzii va fi mai mica decat valoarea matematica calculata. Intre rata nominala a dobanzii, r, rata reala a dobanzii, r_r , si rata inflatiei, i_e , exista relatia:

r = r_r + i_e + r_r · i_e

Pentru valori mici (sub 10%) ale lui r_r si i_e , expresia de mai sus se simplifica si se poate scrie:

r = r_r + 1

rata nominala a = rata reala a + rata acteptata

dobanzii    dobanzii a inflatiei

Rata reala a dobanzii este constanta, in timp ce rata inflatiei se modifica si ca rata nominala a dobanzii se modifica pe masura ce se modifica rata inflatiei, este cunoscuta sub denumirea de efect Fisher, dupa numele celui care l-a pus in evidenta, Irving Fisher.

7. Scont versus dobanda

Scontul (discontul) este valoarea cu care se reduce valoarea nominala a unei creante financiare, cum ar fi cambia sau titlul de stat, reprezentand dobanda datorata pentru creanta pe perioada de timp ramasa pana la scadenta acesteia. Diferenta dintre scont si dobanda consta in faptul ca dobanda se adauga la capital, in timp ce scontul se scade din capital.

Rata scontului este rata dobanzii folosita la determinarea scontului la vanzarea unui instrument financiar.

Veniturile si cheltuielile aferente operatiunii de scontare sunt similare cu veniturile si cheltuielile care rezulta din calculul dobanzii. Diferenta este ca, in timp ce plata/incasarea dobanzii este realizata, de obicei, in timpul sau la sfarsitul perioadei tranzactiei financiare, veniturile si cheltuielile aferente operatiunii de scontare apar, de regula la inceputul perioadei tranzactiei.

8. Tipuri de scadente si modul de calcul al dobanzii

In practica bancara modul de calcul al dobanzii este diferentiat in functie de tipul scadentelor, care pot fi unice sau esalonate in timp.

a) in cazul scadentelor unice, calculul dobanzii se poate face direct prin utilizarea tabelelor care cuprind coeficientii de capitalizare (factori de compunere) sau cu ajutorul formulei dobanzii simple.

b) in cazul scadentelor esalonate in timp exista urmatoarele metode de calcul al dobanzii:

- calculul regresiv al dobanzii (descrescatoare in timp);

- calculul progresiv al dobanzii (crescatoare in timp);

- dobanda egal distribuita in timp pe fiecare rata scadenta;

- amortizarea creditelor.

Calculul regresiv al dobanzii se caracterizeaza prin aceea ca dobanda platita in timp, pe toata perioada creditarii, este mai mare in primii ani (sau luni) si mai mica in anii (lunile) din urma, distribuita in timp pe ratele scadente. In acest caz, dobanda se calculeaza asupra valorii nerambursate a creditului.

Calculul progresiv al dobanzii se individualizeaza prin aceea ca dobanda platita in timp este mai mica la inceput si mai mare la sfarsitul ratelor scadente. Rata dobanzii se aplica la fiecare rata scadenta, luandu-se in considerare intreaga perioada scursa de la acordarea creditului pana la fiecare scadenta si se calculeaza la valoarea rambursata a creditului.

Dobanda egal distribuita in timp pe fiecare rata scadenta se poate calcula prin doua metode:

- metoda bazata pe perioada medie de creditare;

- metoda utilizand coeficientului de restituire a imprumutului.

Metoda bazata pe perioada medie de creditare presupune:

- calcularea perioadei medii de creditare cu ajutorul formulei:

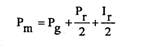
unde:

Pm = perioada medie de creditare;

Pg = perioada de gratie (vacanta);

Pr = perioada de rambursare;

Ir = intervalul dintre doua rambursari consecutive.

- calcularea dobanzii pentru intreaga valoare a creditului (nu pentru fiecare rata ca in cazul celorlalte metode);

- repartizarea in mod egal a dobanzii pe ratele scadente.

Amortizarea imprumuturilor presupune rambursarea acestora in sume periodice egale (lunar, trimestrial etc.). Formula folosita este cea derivata din formula valorii prezente a unei anuitati ordinare:

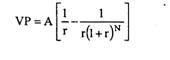
unde, A este anuitatea, iar r este rata dobanzii (rata de actualizare).