Prelucrarea preliminara a masuratorilor geodezice. Obiectivele principale ale prelucrarii preliminare constau in determinarea elementelor necesare construirii modelului functional-stochastic al prelucrarii propriu-zise, precum si in centrarea si reducerea observatiilor geodezice la o suprafata de referinta unitara.

Asa cum este cunoscut din cap. 4, realizarea retelelor geodezice de indesire se bazeaza pe principiul ierarhic. Conform acestui principiu se poate emite ipoteza ca in reteaua geodezica de indesire exista un numar oarecare (egal sau mai mare cu cel necesar si suficient) de puncte cu coordonate cunoscute, determinate in retelele geodezice mai vechi.

Pentru centrarea si reducerea observatiilor geodezice la suprafata de referinta este necesara determinarea unor coordonate de lucru, numite coordonate preliminarii, pentru a le deosebi de coordonatele provizorii, cu care se opereaza efectiv in prelucrarea propriu-zisa. Calculul coordonatelor preliminarii se efectueza cu un numar restrans de cifre, dependent de aproximatia de calcul acceptata si de lungimea laturilor retelei planimetrice. In acest scop se vor parcurge anumite etape de calcul care se vor repeta si la determinarea coordonatelor provizorii.

1. Calculul distantelor D si al orientarilor q intre punctele vechi din reteaua geodezica. Prima etapa de calcule este constituita de calculul distantelor D si al orientarilor q intre punctele vechi din retea, care pot fi denumite elemente initiale de baza. De reamintit ca marimea acestora nu se va modifica prin prelucrare. Considerand, pentru exemplificare, doar doua puncte vechi A si B (Fig. 1.) se poate scrie:

(4)

unde: (5) Fig. 1. Orientarea q si distanta D intre doua puncte vechi.

Deoarece elementele initiale, calculate cu relatiile de mai sus, intervin in foarte multe calcule ulterioare, este necesara o precizie deosebita in calculul acestora si un control corespunzator. Acest principiu, de verificare permanenta a calculelor, este specific prelucrarilor riguroase efectuate in geodezie.

In cazul examinat, controlul este realizat prin utilizarea urmatoarelor relatii:

(6)

Calculele se ordoneaza ca in Tabelul 1. in care sunt obtinute atat rezultatele D si q cat si controalele aferente.

2. Orientarea statiilor cu coordonate cunoscute. Se presupune ca din punctul vechi P (Fig. 2.) au fost vizate punctele vechi A, B, C precum si punctul nou 1.

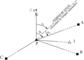Fig. 2. Orientarea statiei P, cu coordonate cunoscute.

In Fig. 2. au fost desenate si unele marimi care se vor cunoaste abia dupa terminarea prelucrarii: - valoarea compensata a masuratorii ; - unghiul de orientare al statiei P.

In aceasta etapa preliminara a calculelor se cunosc:

orientarea , determinata asa cum s-a tratat in 1.;directia masurata .

Nota. Pentru a nu se incarca desenul, nu s-au trecut marimile cunoscute din statia P catre celelalte puncte geodezice vechi B, C, care au insa semnificatii similare cu cele mentionate mai sus.

Daca se determina diferente de forma:

J = A, B, C, (7)se obtin trei valori apropiate ca marime pentru unghiul de orientare a statiei P, care difera insa intre ele: (8)

Diferentele mentionate au doua surse:erorile de masurare care intervin in directiile din relatia (7):

erorile de determinare a coordonatelor punctelor geodezice vechi, care sunt neglijate in conceptia ierarhica.

A orienta o statie P, cu coordonate cunoscute, inseamna a determina media ponderata a valorilor obtinute cu (7):

(9) unde cu (J = A, B, C) s-au notat valorile aproximative (exprimate in kilometri) ale distantelor calculate din coordonatele punctelor vechi.Calculele la proiectul de an pentru orientarea statiilor cu coordonate cunoscute se pot ordona ca in Tabelul 2.

3. Vize orientate preliminar. Unghiul preliminar de orientare a statiei P, notat, se poate utiliza pentru determinarea vizelor orientate preliminar, cu relatii de urmatoarea forma: (10)unde reprezinta directia masurata din statia P catre punctul geodezic nou 1.Desigur, dupa orientarea preliminara a statiilor vechi A, B, C, . din retea se obtin valorile preliminare ale unghiurilor de orientare ale acestor statii si, in continuare, vizele orientate preliminar spre punctul 1 notate, . Asemanator se va proceda cand reteaua geodezica de indesire contine mai multe puncte vechi D, E, F, . si, desigur, mai multe puncte noi 2, 3, 4, . .Rezultatele obtinute la proiectul de an pot fi concentrate ca in Tabelul 3.

4. coordonate (preliminarii) ale punctelor noi. In reteaua geodezica de indesire considerata, exista intotdeauna posibilitati de determinare a coordonatelor punctelor noi prin metoda intersectiei simple inainte (asa cum s-a expus in 4.4.2.2.).

In interiorul fiecarei intersectii se utilizeaza controlul pentru determinarea celei de a doua coordonate, cum ar fi de exemplu:

(valori duble, congruente).    (11)

Cele doua posibilitati de determinare a coordonatei trebuie sa furnizeze marimi congruente, deoarece doua drepte orientate se intersecteaza in plan intr-un punct.

Desigur daca se determina coordonatele preliminarii ale aceluiasi punct geodezic 1 din alta pereche de puncte vechi (de exemplu din B si C) se vor obtine, dupa aceeasi schema de calcul (11) alte valori si respectiv (cu controlul aferent: valori duble, congruente). Acestea difera de perechea de coordonate determinata anterior, datorita influentelor erorilor de masurare. Acestea intervin in unghiurile preliminare de orientare a statiilor vechi si ca urmare si in vizele orientate preliminar:

In ipoteza unor calcule corecte, cele doua serii de coordonate preliminarii obtinute: (12)difera cu maximum 1-2 dm. Media aritmetica a valorilor corespondente poate fi acceptata ca rezultat final.Calculul coordonatelor preliminarii ale punctului 1, din cadrul proiectului de an, pot fi prezentate ca in Tabelul 4., iar coordonatele preliminarii medii ca in Tabelul 5.

Nota

Intr-o retea geodezica de mai mari dimensiuni, unde intervin mai multe puncte noi 1, 2, 3, . se va utiliza urmatoarea modalitate de determinare a coordonatelor preliminarii:

se determina, pentru inceput, punctele noi care au legaturi mai multe (minimum doua) la punctele vechi A, B, C, . ;

in cazul respectarii controalelor mentionate anterior, punctul nou considerat va putea fi folosit, in continuare, la determinarea celorlalte puncte noi din retea, indeplinind un rol asemanator cu cel al punctelor vechi.

5. Corectiile de centrare si de reducere sunt generate de imperfectiunile in realizarea semnalizarii punctelor geodezice, precum si de influentele ulterioare ale factorilor atmosferici ( . .). Ca urmare, cele trei puncte caracteristice ale unui semnal geodezic: C - centrul bornei, I - centrul pilastrului, S - partea vizata a piramidei de semnalizare nu se afla pe aceeasi verticala.

Corectiile de centrare sunt generate de faptul ca I C si se determina cu relatia:

, unde M este masuratoarea efectiva facuta din I.

Corectiile de reducere sunt generate de faptul ca S C si se determina cu relatia:

.

Daca se are in vedere viza P P₁, corectiile de centrare se calculeaza cu elementele din foaia de centrare a statiei P si se aplica masuratorilor din aceasta statie. Corectia de reducere se aplica masuratorii P₁ P, dar determinarea acestora se realizeaza cu ajutorul foii de centrare din punctul geodezic P.

Nota

Distantele necesare la calculul corectiilor de centrare si reducere se deduc, in aceasta etapa, din coordonatele preliminarii (ale punctelor noi) respectiv din coordonatele punctelor vechi, dupa metoda prezentata in 1.

La proiectul de an care se va rezolva in anul III, studentii primesc ca date initiale directii centrate si reduse la planul de proiectie in punctul de statie. De aceea in manualul prezent nu se va intra in detaliile de calcul aferente, care ar necesita un spatiu editorial prea mare (cititorul interesat este indrumat catre manualul scris de Ghitau, 1983, pg. 376).

Corectia de reducere la planul de proiectie (sau de reducere la coarda) notata d_ij - pentru directia masurata din punctul geodezic P_i catre un alt punct geodezic P_j. Determinarea acestei categorii de corectii este explicata in cadrul cursului de Cartografie matematica. In calcule se vor folosi fie coordonatele punctelor vechi, fie coordonatele preliminarii ale punctelor noi, in functie de situatia concreta.

1.2. Coordonatele provizorii ale punctelor noi se determina conform urmatorului algoritm:

directiile masurate in statie sunt corectate cu corectiile de centrare c si de reducere r, asa cum s-a prezentat in 5., precum si cu corectiile de reducere la planul de proiectie d_ij. Pentru simplificarea notatiilor, directia masurata, centrata si redusa la planul de proiectie din punctul de statie P_i catre un alt punct geodezic P_j din retea se va nota in continuare cu

cu aceste directii se determina alte vize orientate (3.) prin utilizarea acelorasi unghiuri de orientare

coordonatele provizorii ale punctelor noi se calculeaza analog ca in 4., folosind insa noile vize orientate. In ipoteza unor calcule efectuate corect, controalele mentionate in 4. sunt mai bine indeplinite.

1.3. Alte elemente provizorii. Din coordonatele provizorii ale punctelor geodezice noi din retea si (dupa caz) din coordonatele x, y ale punctelor geodezice vechi se calculeaza (dupa indicatiile din 1.):

distantele provizorii ;

orientarile provizorii .

Recapituland, elementele provizorii necesare in prelucrarea propriu-zisa sunt: coordonatele provizorii ale punctelor geodezice noi , , distantele si orientarile provizorii notate D* respectiv q* (intre punctele geodezice noi sau intre un punct geodezic nou si un punct geodezic vechi).

Orientarile si distantele provizorii intre punctele geodezice vechi A, B, C, D si punctul geodezic nou 1, la proiectul de an, se pot prezenta ca in Tabelul

2. Sisteme echivalente de ecuatii ale corectiilor

Forma generala a modelului functional-stochastic care sta la baza prelucrarii observatiilor efectuate in retelelele geodezice prin metoda observatiilor indirecte a fost prezentata in 4.1.1.. In continuare se va examina in detaliu aplicarea acestor principii in cazul retelelelor planimetrice, tinand seama de particularitatile acestora.

Doua sisteme de ecuatii ale corectiilor se numesc echivalente daca le corespund unul si acelasi sistem de ecuatii normale si, prin urmare, conduc la obtinerea acelorasi valori pentru necunoscutele pe care le contin.

Se vor examina mai jos trei situatii intalnite foarte des la prelucrarea masuratorilor efectuate in retelele planimetrice geodezice, cunoscute si sub denumirea de reguli ale lui Schreiber care vor aduce importante simplificari de calcul.

2.1. Situatia 1 de echivalenta. Se considera urmatorul sistem de ecuatii ale corectiilor:

pondere p₁;

pondere p₂; (13) .

pondere p_n.

Se observa ca necunoscuta dz are coeficientul -1 in toate ecuatiile. Sistemul (13) poate fi inlocuit printr-un sistem echivalent (14), care are un numar de n+1 ecuatii, insa din care lipseste necunoscuta dz:

pondere p₁;

pondere p₂;

pondere p_n; pondere

Ultima ecuatie a sistemului (14) este denumita ecuatie suma. Pentru demonstrarea echivalentei urmarite, se formeaza sistemul de ecuatii normale corespunzator sistemului (13):

. . (15)

Se deduce necunoscuta dz din prima ecuatie normala:

(16)

si se introduce in celelalte ecuatii. In acest fel se obtine:

. .

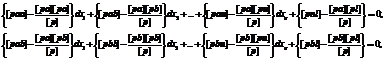
Formand direct ecuatiile normale ale sistemului (14), vor rezulta aceleasi ecuatii (17), ceea ce demonstreaza echivalenta cautata.

2.2. Situatia 2 de echivalenta. Fie un sistem de k ecuatii ale corectiilor, cu aceiasi coeficienti ai necunoscutelor x, insa cu termenii liberi diferiti. Ecuatiile au ponderi diferite.

pondere p₁;

pondere p₂;

pondere p_k.

Acest sistem este echivalent cu urmatoarea ecuatie:

pondere (19)

in care termenul liber este media ponderata a termenilor liberi din sistemul (18) iar ponderea sa este egala cu suma ponderilor ecuatiilor (18).

Intr-adevar, sistemului (18) ii corespunde urmatorul sistem de ecuatii normale:

(20)

Ecuatiei (19) ii corespunde acelasi sistem de ecuatii normale.

Observatie. Este de observat ca aceasta demonstratie este posibila numai in situatia in care numarul total al ecuatiilor de corectii ramane mai mare ca numarul necunoscutelor. Aceasta presupune ca situatia examinata se intalneste intr-un cadru mai general, intr-o prelucrare in care intervin mult mai multe ecuatii decat cele avute in vedere. O formulare mai exacta a cestei reguli ar fi: un sistem particular de ecuatii de corectii de forma (18), care este parte componenta a unui sistem mult mai mare, poate fi inlocuit de ecuatia (19.) inainte de trecerea la sistemul de ecuatii normale corespondent deoarece contributia acestora este aceeasi.

2.3. Situatia 3 de echivalenta. Ecuatia

pondere p (21)

poate fi adusa la ponderea egala cu 1, daca intreaga ecuatie este multiplicata cu . Demonstratia acestei situatii este cunoscuta de la cursul Prelucrarea masuratorilor geodezice. O alta posibila demonstratie este data de aplicarea acelorasi rationamente ca la celelalte situatii de echivalenta, expuse anterior, prin acceptarea ipotezei mentionate in observatie.

In geodezie intervine si cazul particular in care o ecuatie de corectie de ponderea p, cum ar fi de exemplu ecuatia (21) se imparte cu o anumita constanta k. Evident, ponderea noii ecuatii se modifica in mod corespunzator:

; pondere (22)

Demonstratia este imediata: daca ecuatia (22) se inmulteste cu se obtine ecuatia (21), cu ponderea p.

3. Variatia orientarii q* in functie de variatiile coordonatelor plane 3.1. Cazul general. Coordonatele provizorii ale punctelor noi , din Fig. 3., aflate in legatura directa si reciproca intr-o retea de triangulatie, vor primi prin compensare anumite corectii:

(23)

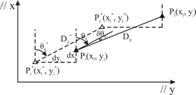
Fig. 3. Variatiile orientarii si distantei in functie de variatiile coordonatelor plane Ca urmare, orientarea provizorie va primi o modificare care este functie de corectiile dx si dy ale punctelor considerate:

(24)

In sistemul de axe adoptat rezulta:

(25)

Daca se diferentiaza in ambii termeni ai ecuatiei de mai sus se obtine:

(26)

Tinand seama de formulele (6) si introducand notatiile:

(27) (28)

se obtine din relatia (26):

(29)

Coeficientii a_ij si b_ij se numesc coeficienti de directie, deoarece prin intermediul lor se exprima variatia orientarii pe unitatea de lungime considerata (coeficientul a pe axa x si coeficientul b pe axa y).

Observatii.

Din motive practice, in triangulatia de stat (cu lungimi D* mari) se considera de obicei variatia pe decimetru, iar D, Dx si Dy se exprima in kilometri, astfel incat formulele pentru astfel de situatii sunt (in cazul gradatiei centezimale) urmatoarele:

; . (30)

In asemenea situatii, corectiile dx si dy rezultate din compensare vor fi exprimate in decimetri.

Analog, pentru retele de mici dimensiuni (cu laturi de 1, . 4 km), ca in cazul proiectului de an, se poate opera cu coeficienti de directie de 100 de ori mai mici decat cei din relatia (30) si, ca urmare, corectiile dx si dy vor fi exprimate in milimetri:

  (31)

Formulele (31) sunt recomandabile pentru rezolvarea temei proiectului de an. Calculele si controalele aferente se pot prezenta ca in Tabelul 7..

Controlul calculelor coeficientilor de directie este dat de:

sau . (32)

Din relatiile (26) si (27) rezulta:

; . (33)

Deoarece , vom avea:

(34)

3.2. Cazuri particulare

3.2.1. Intersectia inainte. Se considera ca punctul P_i este punct vechi, cu coordonate cunoscute, asfel incat dx_i = dy_i = 0 si, ca urmare, expresia (29) devine:

. (35)Este bine sa se retina si o regula practica pentru deducerea semnelor coeficientilor necunoscutelor dx_j si dy_j in cazul intersectiei inainte: la orientarea se adauga 100^g si semnele acestor coeficienti vor fi identice cu semnele pe care le au axele de coordonate in cadranul obtinut.

Intersectia inapoi. Se considera ca punctul P_j este vechi, cu coordonate cunoscute, astfel incat dx_j = dy_j = 0 si, ca urmare, expresia (29) devine:

. (36)

Aceasta este relatia specifica intersectiei inapoi, cand dq este calculat in punctul nou P_i.Se poate retine si aici o regula practica pentru deducerea semnelor coeficientilor necunoscutelor si : din orientarea se scade 100^g si semnele acestor coeficienti vor fi identice cu semnele pe care le au axele de coordonate in cadranul obtinut.

Ambele puncte sunt noi. Putem sa privim acum cazul general, examinat initial (formula (29)), ca o insumare a celor doua cazuri particulare de mai sus. Se vor putea astfel aplica, pe rand, cele doua reguli practice privind stabilirea semnelor coeficientilor necunoscutelor.

2.3.4. Ambele puncte sunt vechi. Avem evident dq

3. Variatia distantei in functie de variatiile coordonatelor plane

Revenind la Fig. 3. se poate scrie:

(37)

Prin diferentiere se obtine:

(38)

Daca se folosesc relatiile (6), adaptate corespunzator situatiei analizate:

relatia (38) se scrie mai simplu:

(40)

In acest mod se determina cantitatea dD_ij cu care se modifica prin prelucrare distanta provizorie in raport de modificarile coordonatelor provizorii (dx_i, dy_i, dx_j, dy_j) ale celor doua puncte considerate.

Observatii Coeficientii necunoscutelor dx_i, dy_i, dx_j, dy_j din relatia (40) au valori subunitare (egale cu valorile functiilor trigonometrice sinus si cosinus) astfel incat nu mai sunt necesare operatii suplimentare de omogenizare (asa cum s-a procedat cu ecuatia (29)).

Pentru a se pastra legatura dintre ecuatiile de corectii pentru directii si respectiv pentru distantele masurate, toate marimile metrice (dx, dy, , , , dD) care intervin in aceste ecuatii se vor exprima in aceeasi unitate de masura (in cazul proiectului de an - in milimetri).

In mod evident,

dD_ij s dD_ji, (41)

deoarece distanta dintre doua puncte este unica. Prin urmare, ecuatia (40) se poate scrie fie in punctul de statie P_i, fie in punctul vizat P_j, cu modificarile de indici corespunzatoare. Astfel, de exemplu, ecuatia corespondenta pentru o distanta masurata in punctul vechi A catre punctul nou 1 are forma:

(42)

Aceasta ecuatie este identica cu ecuatia scrisa in punctul nou 1 catre punctul vechi A:

(43)

Deoarece rezulta ecuatia corespondenta formulei (41): dD_A1 s dD_1A.

Deoarece coordonatele punctelor vechi nu se modifica prin prelucrare (principiul ierarhic),

dD_BC = 0. (44)

De aceea, in retelele geodezice de indesire nu se masoara distante intre punctele vechi.

4. Forme ale ecuatiilor corectiilor

4.1. Directii centrate si reduse la planul de proiectie. Din punctul de statie P s-au vizat punctele de triangulatie 1, 2, . , n (Fig. 4), rezultand - directii centrate si reduse la planul de proiectie. Acestea urmeaza a fi corectate in procesul de prelucrare:

; (j = 1, 2, . , n).    (45)

Se presupun cunoscute, de asemenea, orientarile provizorii . Diferentele de forma (7.), in care se presupune cunoscuta o valoare provizorie a unghiului de orientare:

(46)

conduc la urmatorul sistem de ecuatii ale corectiilor:

; (j = 1, 2, . , n)    (47)

unde s-au notat:

; (j = 1, 2, . , n).    (48)

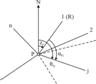
Fig. 4. Determinarea unghiului de orientare provizoriu.

Pentru determinarea valorii provizorii a unghiului de orientare se pot folosi diverse procedee. Este util din punct de vedere practic sa se convina ca suma termenilor liberi ai ecuatiilor corectiilor, scrise pentru o statie oarecare, sa fie zero:

(49)

Pe baza acestei conventii rezulta prin insumarea relatiilor (48):

. (50)

Observatii

Unghiul de orientare provizoriu se obtine ca medie aritmetica simpla a unghiurilor de orientare obtinute pentru toate directiile masurate in statie.

Termenii liberi ai ecuatiilor corectiilor se obtin ca diferente intre unghiurile de orientare individuale si unghiul de orientare provizoriu [v. relatiile (48)].

In toate ecuatiile corectiilor, necunoscuta dz are coeficientul (- 1) [v. sistemul (47)].

In functie de caracterul variatiei orientarii dq, se pot intalni urmatoarele tipuri de ecuatii ale corectiilor in cazul compensarii directiilor masurate:

pentru o directie masurata in punctul vechi A catre punctul vechi B:

(51)

pentru o directie masurata in punctul A catre punctul nou j:

(52)

pentru o directie masurata in punctul nou j catre punctul vechi B:

(53)

pentru o directie masurata in punctul nou k catre punctul nou j:

(54)

Asa cum s-a studiat la cursul Prelucrarea masuratorilor geodezice, numarul ecuatiilor de corectie este egal cu numarul masuratorilor geodezice. Pentru o ordonare convenabila a calculelor, ecuatiile corectiilor se scriu pe statii (de regula se incepe cu statiile din punctele vechi si in final cu cele din punctele noi). Se incepe cu directia de referinta (R) asa cum s-a procedat si in 5.9.1.3., continuandu-se in sens orar cu toate masuratorile din statie (spre puncte geodezice vechi sau noi).

4.2. Distante masurate si reduse la planul de proiectie. Ecuatia de corectie aferenta acestui tip de masuratori este dedusa din egalitatea:

(55)

in care reprezinta corectia aferenta distantei masurate si redusa la planul de proiectie. Indicele superior D la corectia separa aceasta corectie de - care reprezinta corectia pentru directia masurata din punctul geodezic P_i spre punctul geodezic P_j.

In functie de forma pe care o are dD_ij (3.) se pot intalni urmatoarele tipuri de ecuatii ale corectiilor in cazul masurarii distantelor:

distanta masurata intre punctul geodezic vechi A si punctul geodezic nou 1:

, (56)

unde:

. (57)

Reamintim: D* sunt distante provizorii calculate din coordonate provizorii iar D⁰ sunt distante masurate.Asa cum s-a mentionat deja in 3., daca ecuatia aferenta acestui gen de masuratori se scrie din punctul geodezic 1 catre punctul geodezic vechi A, rezulta:

. (58)Deoarece si rezulta evident .

Nota

Potrivit principiului continut de observatia 5 de mai sus, pentru o distanta masurata se scrie o singura ecuatie de corectie (de forma (56) sau (58));

pentru distanta masurata intre punctele geodezice noi 2 si 3 se alege una dintre urmatoarele posibilitati:

; (59)

; (60)

;    (61)

;    (62)

deoarece in retelele geodezice de indesire nu se masoara distante intre punctele geodezice vechi, nu exista corectii de forma (S, J = A, B, . ).

5. Intersectia multipla inainte. Din mai multe puncte vechi din reteaua de triangulatie se efectueaza observatii azimutale catre un punct nou, precum si catre alte puncte vechi din retea (pentru orientarea cat mai buna a statiilor); punctul nou nu este stationabil. Asemenea situatii intervin in special la indesirea retelelor de triangulatie cu puncte greu stationabile (biserici, turnuri cu diverse destinatii s.a.), care sunt insa deosebit de utile in ridicarile topografice ulterioare, deoarece sunt usor vizibile, chiar de la distante mari.Se cere prelucrarea prin metoda celor mai mici patrate a masuratorilor efectuate.Se accepta ca in punctele geodezice vechi A, B, C, . , F (Fig. 5.) au fost efectuate observatii azimutale de aceeasi precizie. Se considera cunoscute coordonatele provizorii ale punctului nou P si, prin urmare, si orientarile provizorii, precum si coeficientii de directie a si b.

5.1. Ecuatiile initiale ale corectiilor. Sistemul ecuatiilor corectiilor, scris in fiecare din punctele vechi, va cuprinde mai multe ecuatii de tipul (51) si doar o singura ecuatie de tipul (52). Astfel, pentru statia A rezulta: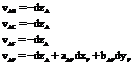 (63)

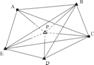
Fig. 5. Intersectia multipla inainte.

5.2. Transformarea ecuatiilor corectiilor cu regulile de echivalenta Schreiber. Sistemul de ecuatii de corectie (63) se incadreaza in situatia 1 de echivalenta (2.1.) deoarece necunoscuta dz_A are coeficientul - 1 in toate ecuatiile sistemului. Asa cum s-a demonstrat in 2.1. acest sistem se poate inlocui cu un sistem de ecuatii ale corectiilor din care lipseste necunoscuta dz_A, dar intervine o ecuatie in plus, denumita ecuatia suma. Aceasta regula generala aplicata in cazul de fata aduce simplificari remarcabile:

in viitorul sistem de ecuatii ale corectiilor nu mai intervin ecuatiile specifice pentru deoarece acestea nu mai contin necunoscute;

ecuatia suma se scrie deosebit de usor deoarece se vor avea in vedere doar coeficientii ultimei ecuatii din sistemul (63). In plus, termenul liber aferent ar avea forma si devine zero deoarece , ca in orice alta statie S.

Aceste rationamente, ne conduc la urmatorul sistem de doar doua ecuatii echivalente ale corectiilor, in care intervin doar doua necunoscute:

unde cu n_A s-a notat numarul total de directii masurate in statia A (in exemplul considerat n_A = 4).Pentru calculele ulterioare este util ca ultima ecuatie din sistemul (64) sa fie impartita cu p_A. Ca urmare (2.3.), ponderea ecuatiei se va modifica cu , rezultand:

(65)Sistemul de ecuatii (65) indeplineste conditiile situatiei 2 de echivalenta (2.2.) deoarece necunoscutele pe care le contine au aceiasi coeficienti in ambele ecuatii. Acest sistem poate fi inlocuit printr-o singura ecuatie, care are termenul liber si ponderea , care se pot calcula cu regulile stabilite in 2.2.:

(66)

(67)

(68)

Prin urmare, aplicand corespunzator regulile de echivalenta Schreiber, in fiecare statie A, B, C, . , F se obtine o micsorare semnificativa a numarului de ecuatii. Indiferent de numarul de ecuatii initiale de forma (63) se obtine in final doar o singura ecuatie transformata pentru fiecare statie, de forma (66) care se poate scrie cu usurinta. Si numarul de necunoscute s-a micsorat foarte mult, ecuatiile finale avand in structura lor doar necunoscutele de pozitie dx_P, dy_P ale punctului geodezic nou P. Necunoscutele de orientare ale statiilor vechi dz_A, dz_B, dz_C, . , dz_F care au fost eliminate in aceasta etapa de calcule se vor determina ulterior cu ecuatii de forma (72).

5.3. Calculul marimilor compensate. In exemplul avut in vedere, din ecuatiile transformate ale corectiilor de forma (66), se obtin doua ecuatii normale cu doua necunoscute:

(69)

Asa cum se cunoaste de la cursul Prelucrarea masuratorilor geodezice sistemul (69) se rezolva comod cu metoda Gauss a eliminarilor succesive, intr-o schema de calcul care include controale specifice, inclusiv pentru calculul solutiilor dx_P, dy_P.Pentru evaluarea preciziei obtinute la metoda intersectiei multiple inainte, la schema mentionata se adauga doua coloane suplimentare care vor servi la calculul coeficientilor de pondere .Pentru determinarea necunoscutelor de orientare a statiilor A, B, C, . , F se utilizeaza prima dintre ecuatiile:

[pav] = [pbv] = . = [puv] = 0, (70)cunoscute de la cursul de Prelucrarea masuratorilor geodezice (conditiile de trecere de la sistemul ecuatiilor de corectie la sistemul ecuatiilor normale).Aplicand prima conditie din (70) la sistemul (61) si avand in vedere ca necunoscuta dz_A are coeficientul - 1 in toate ecuatiile, iar ponderile acestora sunt egale cu , rezulta o alta conditie si anume:

(71)

valabila in oricare dintre statiile A, B, C, . , F.

Prin utilizarea conditiei (71) la sistemul (61) rezulta: (72)

Analog se determina si celelalte necunoscute dz_B, dz_C, . , dz_F.

Corectiile v cu care urmeaza sa se determine directiile compensate se calculeaza din ecuatiile initiale ale corectiilor, de forma (61).

Analog cu (4.29) se poate scrie: (73)De asemenea, analog cu (4.35) se deduc valorile compensate ale necunoscutelor care intervin la intersectia multipla inainte: (74)

5.4. Estimarea preciziei. Matricea inversa a sistemului ecuatiilor normale , care are forma generala din Tabelul 4.1., are un aspect foarte simplu in cazul intersectiei multiple inainte:

(75)

Coeficientii de pondere din matricea (75) se obtin odata cu rezolvarea sistemului ecuatiilor normale si sunt folositi la evaluarea preciziei.

Formulele de calcul au fost prezentate in 4.4.1.1.:

abaterea standard a unitatii de pondere s₀:, (4.59)unde:

marimea [pvv] se determina prin calcul direct, utilizand corectiile v calculate din sisteme de ecuatii de forma (61) iar ponderile p sunt cunoscute. Deoarece aceasta marime are un rol important in evaluarea preciziei, este indicat sa se utilizeze si formula de control cunoscuta de la cursul Prelucrarea masuratorilor geodezice:

[pvv] = [pll] + [pal]x_P + [pbl]y_P;    (76)

Abaterile standard ale coordonatelor precum si abaterile standard totale:

; (4.55); (4.56); (4.57)

Elementele elipsei erorilor:

; (4.63) ; (4.64) . (4.65)

Abaterea standard a unei masuratori . (77)

5.5. Controlul prelucrarii. Exactitatea prelucrarii este data de verificarea urmatoarei ecuatii, pentru oricare dintre directiile masurate:

, (78)in care se calculeaza din coordonatele compensate (74), - din aceleasi relatii iar din formulele (73).Un exemplu numeric complet privind prelucrarea masuratorilor geodezice efectuate pentru intersectia multipla inainte, util pentru rezolvarea temei proiectului de an III, este prezentat in Tabelele 8. .

Intersectia multipla inapoi

Intr-un punct nou din reteaua de triangulatie se efectueaza observatii azimutale catre mai multe puncte vechi din retea, care nu pot fi stationate. Se cere prelucrarea prin metoda celor mai mici patrate a masuratorilor efectuate.Asemenea situatii sunt, in general, evitate in triangulatia de stat, deoarece posibilitatile de orientare a statiei sunt mai limitate decat la intersectia multipla inainte; orientarea statiei se va realiza numai prin utilizarea punctelor cu care exista legatura directa. Metoda intersectiei multiple inapoi este folosita pe cale larga in retelele de triangulatie utilizate la trasarea unor constructii masive.Se considera ca din punctul nou P (Fig. ) au fost masurate (cu aceeasi precizie) directii catre puncte vechi A, B, . , F, care din diverse motive nu pot fi stationate.

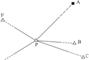Fig. Intersectia multipla inapoi.

Sistemul de ecuatii ale corectiilor, scris pentru punctul P, va fi

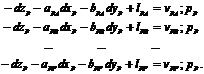
Referitor la sistemul de ecuatii de corectii de mai sus se pot face urmatoarele observatii:

calculul elementelor provizorii (I = A, B, . , F) a fost tratat in 1. si poate fi adaptat cu usurinta la situatia intersectiei multiple inapoi;

coeficientii de directie (I = A, B, . , F) se determina ca in 3.. Calculele la proiectul de an se pot prezenta ca in Tabelul 7.;

termenii liberi (I = A, B, . , F) se determina cu relatiile (47) astfel incat se respecta conventia (49), ca in oricare alt punct de statie;

analog cu constatarile din 5.2., si in sistemul (78) necunoscuta dz are coeficientii

- 1 in toate ecuatiile, care la randul lor sunt caracterizate de aceeasi pondere . In aceste conditii se respecta conditia (71).

Utilizand conditiile , se poate elimina necunoscuta inainte de formarea ecuatiilor normale :

(80)

Daca se noteaza:

; I = A, B, . , F, (81)rezulta urmatorul sistem de ecuatii transformate ale ecuatiilor corectiilor, in care intervin noi coeficienti de directie denumiti coeficienti de directie transformati:

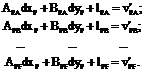(82)

La calculul coeficientilor de directie transformati se vor folosi si posibilitatile de control, derivate din proprietatea cunoscuta a mediei aritmetice:

(83)

Sistemul de ecuatii normale obtinut din sistemul ecuatiilor transformate ale corectiilor (81) are forma:

(84)

Din acest stadiu, calculele decurg analog ceea ce s-a mentionat la intersectia multipla inainte, desigur cu adaptarile corespunzatoare:

calculul marimilor compensate, ca in 5.3.;

estimarea preciziei, ca in 5.4..

Observatie

La calculul abaterii standard a unitatii de pondere cu relatia (4.59) in cazul retelelor geodezice de indesire, defectul de rang d = 0. Numitorul fractiei de sub radical trebuie sa ramana pozitiv. Deoarece la intersectia multipla inapoi numarul de necunoscute u = 3, rezulta o conditie care trebuie respectata de numarul de masuratori:. (85)

In situatia intersectiei simple inapoi (utilizata in topografie) se admite n = 3 (numarul de masuratori strict necesare si suficiente efectuate in punctul nou P in aceasta situatie).

Un exemplu numeric complet privind prelucrarea masuratorilor geodezice efectuate pentru intersectia multipla inapoi, util pentru rezolvarea temei proiectului de an III, este prezentat in Tabelele 17-23.

7. Intersectia multipla combinata

Asa cum rezulta si din denumire, in cadrul intersectiei multiple combinate se realizeaza o unificare a principiilor de determinare expuse in cadrul intersectiilor multiple inainte si, respectiv, inapoi. Ilustrativ situatia este prezentata de Fig. 7 in care se urmareste, in continuare, determinarea coordonatelor aceluiasi punct P, de aceasta data prin metoda intersectiei multiple combinate.

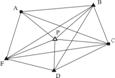
Fig. 7. Intersectia multipla combinata.

Calculele preliminarii, determinarea marimilor provizorii precum si coeficientii de directie (S = A, B, C, . , F) se adapteaza cu usurinta, in functie de regulile stabilite in acest capitol.

Numarul ecuatiilor initiale ale corectiilor este egal cu numarul directiilor masurate, atat in punctele vechi A, B, . , F cat si in punctul nou P. Se observa ca se pot aplica cunostintele anterioare expuse in 5. si .

Forma ecuatiilor initiale ale corectiilor, scrise in punctele vechi, este analoga cu (63). Dupa aplicarea succesiva a regulilor de echivalenta Schreiber, rezulta in fiecare punct vechi o singura ecuatie transformata de forma (66).

In punctul nou P se pot scrie ecuatiile initiale ale corectiilor de forma (78) si dupa aplicarea unei singure transformari se obtin ecuatiile transformate ale corectiilor de forma (82).

Din ecuatiile transformate ale corectiilor, rezultate in punctele vechi A, B, . , F si in punctul nou P se poate forma sistemul ecuatiilor normale specific (2 ecuatii cu 2 necunoscute: Acelasi sistem se poate obtine din insumarea sistemelor de ecuatii normale (69) si respectiv (84). Din acest stadiu, calculele decurg analog cu ceea ce s-a mentionat in 5., desigur cu adaptarile corespunzatoare

calculul marimilor compensate, ca in 5.3.;

estimarea preciziei, ca in 5.4.

Un exemplu numeric complet privind prelucrarea masuratorilor goedezice efectuate intr-o intersectie multipla combinata, utila pentru rezolvarea temei proiectului de an III, este prezentat in Tabelele 24-30.In Tabelul 31 se prezinta rezultatele centralizate obtinute la cele trei aplicatii.

Concluzii

Cele trei metode de prelucrare a masuratorilor geodezice prezentate in acest capitol: intersectia multipla inainte, intersectia multipla inapoi si intersectia multipla combinata furnizeaza rezultate finale diferite, asa cum este prezentat in Tabelul 31. Aceasta afirmatie se refera atat la marimile compensate (coordonatele punctului nou P) cat si la estimatorii de precizie. Rezultatele obtinute la intersectia multipla combinata se bazeaza pe un volum mai mare de masuratori si de aceea prezinta cel mai mare grad de incredere.

Cazul general al prelucrarii masuratorilor geodezice efectuate in retelele planimetrice prin metoda observatiilor indirecte este reprezentat de o situatie mai complexa decat cea avuta in vedere in acest capitol si anume o retea geodezica formata dintr-un numar mai mare de puncte vechi precum si dintr-un numar mult mai mare de puncte noi. Astfel de retele geodezice rezulta in cazul in care suprafata acoperita este mult mai mare in comparatie cu cea avuta in vedere la proiectul de an. In asemenea retele geodezice se masoara nu numai directii orizontale ci si distante, precum si alte marimi mentionate in 4.2. si 4.3.. Se vor aplica principiile de calcul expuse in acest capitol, desigur cu multe adaptari corespunzatoare (Ghitau, 1983, pg. 394-408). O asemenea retea este denumita in lumea de specialitate grup de puncte.