 | Biologie | Chimie | Didactica | Fizica | Geografie | Informatica |
| Istorie | Literatura | Matematica | Psihologie |
Este o structura de date pentru care sunt definite urmatoarele operatii:
insert (S,a) - insereaza un atom in structura,
remove (S) - extrage din structura atomul cu cheia cea mai mare.
O coada cu prioritati poate fi implementata printr-o lista. Implementarea cozii cu prioritati prin lista permite definirea operatiilor insert si remove, in cazul cel mai bun, una este de complexitate O(1) si cealalta este de complexitate O(n).
Implementarea cozii cu prioritati prin heap face o echilibrare cu complexitatea urmatoare: una este de complexitate 0(log n) si cealalta de complexitate 0(log n).
/
heap /
/ 50
/ /
/ 40 30
/ / /
/ 33 37 12 2
/ / / _________
/ 10 15 7 | 42
----- ----- -------|
Acelasi arbore in reprezentare implicita:

Operatiile insert si remove pentru arbori heap au o forma foarte simpla cand utilizeaza reprezentarea implicita. Consideram, in continuare, arbori heap in reprezentare implicita.
Exemplu: un arbore cu ultimul nivel avand toate nodurile aliniate la stanga:
Inseram valoarea 42 T se adauga nodul la un nivel incomplet;
In reprezentarea implicita se adauga nodul la sfarsit.
insert
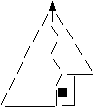
In reprezentarea implicita:
V [N + 1] = a
N = N + 1
In continuare reorganizam structura arborelui astfel incat sa-si pastreze structura de heap.
Se utilizeaza interschimbarile. Comparatii:
Iau 2 indici:
child = N
si
parent = [N/2]
(in cazul nostru N = 11 si [N/2] = 5)
Comparam V[child] cu V[parent].
Interschimbare daca V[child] nu este mai mic decat V[parent] (se schimba 42 cu 37)
Inaintare in sus:
child = parent
parent = [child/2]
Se reia pasul 2) pana cand nu se mai face interschimbarea.
Structura S este un arbore heap. El se afla in reprezentare implicita in 2 informatii:
V vector
N dimensiune
insert(V, N, a) // V vectorul ce contine reprezentarea implicita a heapu-lui;
// N Numarul de noduri din heap, ambele sunt plasate prin referinta (Functia
insert le poate modifica);
// a atomul de inserat;
50
/
45 43
/ /
33 40 40 20
/ /
10 15 7 37 39

se scoate elementul cel mai mare care este radacina heap-ului; se initializeaza cei 2 indici;
se reorganizeaza structura arborilor: se ia ultimul nod de pe nivelul incomplet si-l aduc in nodul-radacina, si aceasta valoare va fi retrogradata pana cand structura heap-ului este realizata.
parent
Conditia de heap /
lchild rchild
parent = max(parent, lchild, rchild).
Exista trei cazuri:
Conditia este indeplinita deodata;
max este in stanga T retrogradarea se face in stanga;
max este in dreapta T retrogradarea se face in dreapta.
remove(V, N)
In cazul cel mai defavorabil se parcurge o ramura care leaga radacina de un nod terminal. La insert avem o comparatie, iar la remove avem doua comparatii. Rezulta, complexitatea este data de adancimea arborelui. Daca N este numarul de noduri din arbore, 2k N 2k+1 , si adancimea arborelui este k+1.
2k - 1 < N 2k+1 - 1 T k = [log2N]
| |
| |
| |
nr. de noduri nr. de noduri
ale arborelui ale arborelui
complet de complet de
adancime k adancime k+1
k log2N < k + 1 T adancimea arborelui este k = [log2N].
Deci complexitatea este O(log N).
A doua aplicatie a heap-urilor este algoritmul Heap_Sort.
Heap_Sort(V, n)
Aceasta procedura sorteaza un vector V cu N elemente: transforma vectorul V intr-un heap si sorteaza prin extrageri succesive din acel heap.
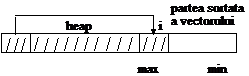
heap_sort
Observatii:
Se fac mai multe operatii insert in heap-uri a caror dimensiune creste de la 1 la N;
Se fac n-1 operatii insert in heap-uri cu dimensiunea N n
Rezulta complexitatea acestor operatii nu depaseste O(n log n). Facem un studiu pentru a vedea daca nu cumva ea este mai mica decat O(n log n)
Cazul cel mai defavorabil este situatia in care la fiecare inserare se parcurge o ramura completa. De fiecare data inserarea unui element se face adaugand un nod la ultimul nivel. Pentru nivelul 2 sunt doua noduri. La inserarea lor se va face cel mult o retrogradare (comparatie).
Pe ultimul exemplu de arbore, avem:
nivelul 2 : 2 noduri 1 comparatie
nivelul : 4 noduri 2 comparatii
nivelul 4 : 8 noduri 3 comparatii
-------- ----- ------ ----- ----- -------
nivelul i : 2i-1 noduri i-1 comparatii
Considerand un arbore complet (nivel complet) T N = 2k - 1 T numarul total de comparatii pentru toate nodurile este T(n) de la nivelul 2 la nivelul k. Vom calcula:
![]()
Sa aratam:
![]()
cu tehnica
![]()
Asadar:

Rezulta:
![]()
iar:
![]()
din
![]()
Rezulta:
![]()
termen dominant
Facandu-se majorari, rezulta complexitatea O(n log n).
Prezentam acum alta strategie de obtinere a heap_gen cu o complexitate mai buna:
Construim heap-ul de jos in sus (de la dreapta spre stanga). Cele mai multe noduri sunt la baza, doar nodurile din varf parcurg drumul cel mai lung.
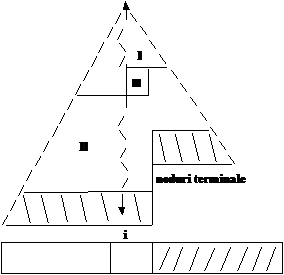
Elementele V[i+1,N] indeplinesc conditia de structura a heap-ului:
j >i avem: V[j] > V[2*j] , daca 2*j N
V[j] > V[2*j +1] , daca 2*j + 1 N
Algoritmul consta in adaugarea elementului V[i] la structura heap-ului. El va fi retrogradat la baza heap-ului (prelucrare prin retrogradare):
retrogradare(V, N, i)
In aceasta situatie, vom avea:
heap_gen
Fie un arbore complet cu n = 2k - 1. Cazul cel mai defavorabil este situatia in care la fiecare retrogradare se parcurg toate nivelele:
nivel k : nu se fac operatii
nivel k-1 : 2k-2 noduri o operatie de comparatie
nivel k-2 : 2k-3 noduri 2 operatii
nivel i : 2i-1 noduri k-i operatii
-------- ----- ------ -------- ----- ------ -
nivel 2 : 21 noduri k-2 operatii
nivel 1 : 20 noduri k-1 operatii
Se aduna, si rezulta:
![]()
Tehnica de calcul este aceeasi:
![]()
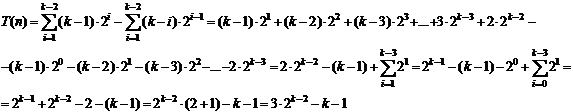
Rezulta:
![]()
![]()
termen dominant
Rezulta complexitatea este O(n). Comparand cu varianta anterioara, in aceasta varianta (cu heap-ul la baza) am castigat un ordin de complexitate. Rezulta, complexitatea algoritmului Heap_Sort este determinata de functiile remove ce nu pot fi aduse la mai putin de complexitate O(log n). Rezulta:
Heap_Sort = O(n) + O(n·log n)
termen ce determina complexitatea
Rezulta complexitatea alg.
Heap_Sort = O(n·log n)
Copyright © 2025 - Toate drepturile rezervate