O metoda alternativa de construire a matricii de control

O metoda alternativa de construire a matricii de control

Detectia unui cuv. La receptie si aprecierea se face pe considerente statistice. Se propune o alta structura particulara pentru matricea de control H.Regula este: primele m coloane ale matricii H vor trebui sa formeze o matrice unitate de rang m, adica:

h₁=; h₂==; . ..h_m==

Toate celelalte coloane:h_m+1=l₁, h_m+2=l₂, h_m+k=l_k; vor fi combinatii liniare ale primelor m. Combinatiile generate trebuie insa sa respecte regula: suma modulo 2 a oricaror 2e coloane distincte sa fie diferita de 0.

Pentru corectia unei singure erori, e=1, trebuie sa avem suma oricaror 2 coloane distincte nenula adica:

(1) l₁=h₁h₂;l₂=h₂h₃; _{. . . . . . ;}l_k=h_kh_k+1

Formarea acestor coloane se termina atunci cand se epuizeaza

toate situatiile atunci cand k+1=m (cazul unei erori).In cazul in care ne propunem sa corectam 2 erori: e=2 sumele din sistemul (1) se vor obtine prin insumarea a cate 4 coloane. Se poate generaliza pt m erori procedura incheindu-se cand e indeplinita conditia: ke+e=m. Pornind de la acest model se pune problema ca la receptie sa se poata determina pozitia unde a aparut eroarea. Pentru aceasta se calculeaza corectorii adica matricea Z:

[Z]]=[H][V']^T

[V^']=[V]

[Z]=[H][ ]^T ceea ce permite identificarea pozitiei und matricea [ ] contine 1 adica identificarea bitilor eronati. Evaluarea cuv receptionat: se considera cunoscute probabilitatile de aparitie a erorii:

p(V'/V)=p^e(1-p)^n-e - probabilitatea aparitiei lui V' daca s-a transmis V;

(1-p) - probabilitatea de transmitere corecta a lui 1;

p= probabilitatea de transmitere corecta a lui 0;

Ca urmare la receptie trebuie alese din multimea cuvintelor receptionateV' acelea care se gasesc la distanta minima Hamming fata de cuvantul transmis.

Se vor scrie succesiv cuvintele eroare in ordinea descrescatoare a ponderii calculandu-se pt fiecare cuv eroare corectorul. Daca rezulta corectori identici se va retine doar cel care corespunde cuv eroare cu ponderea mai mica. Deoarece corectorul poate avea m biti atunci rezulta 2^mcorectori distincti.

EX Sa consideram o matrice de generare a codului cu urm structura:

[H]=Se construiesc cuvintele eroare si se ordoneaza descrescator dupa pondere.

Cuv eroare.

Pondere 0 ->

Pondere 1 -> Pondere 2->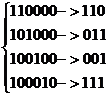

Sa pp ca s-a receptionat un cuv cu structura urm:[v']=[010011].Trebuie sa calculam corectorul Z ca :[Z]=[H][V']^T==> cuvantul receptionat [V'] este corect.

Sa pp ca se receptoneaza un alt cuv: [V']=[1 0 0 0 1 1]. [Z]=[H][V']^T==> [1 1 0]= [Z]^T->001000(pondere 1)

[V]=[V'] [0 0 1 0 0 0]=[1 0 1 0 1 1] care este cel mai probabil cel transmis. Se observa din acest exemplu ca se pot astfel corecta toate erorile singulare indiferent de pozitia pe care apar. Daca in sistem apar insa 2 erori tinand seama ca astfel nu mai avem suficienti corectori distincti=> ca sistemul nu poate rezolva situatia.prin definitie vom numi cod perfect un cod care poate corecta toate combinatiile de e erori sau mai putin. Asta inseamna ca tabelul de decodare construit trebuie sa contina C_n⁰=1 cuvinte eroare cu pondere 0 nenule; C¹_n=n cuvinte eroare de pondere nenule s.a.m.d., C_n^e=cuvinte de pondere e nenule.In cazul codurilor perfecte se atinge cea mai favorabila situatie adica: 2^m=C_n⁰+C¹_n+ . +C_n^e.

In cazul in care se pune problema corectarii unei sg erori: e=1; 2^m=1+n, s-a descoperit un sg cod perfect si anume n=23;m=11;e=3 (cod Galay). Se verifica ca: 2¹¹=C⁰₂₃+C₂₃¹+C₂₃²+C₂₃³

Codurile care pot corecta toate combinatiile de e erori o parte din cuv ce contin e+1 erori si nici una din situatia cu e+2 erori sau mai multe s.n. abaza a 3 parametri:redundanta relative, capacitatea de detectie a erorilor, capacitatea de corectie a erorilor.

Intelegem prin redindanta relativa fractiunea informationala din cuv de cod. Se poate evalua numeric ca fiind: R_r=k/n

Capacitatea de detectie reprezinta raportul dintre nr secventelor detectabile si numarul total de secvente posibile eronate.

Pe baza relatiei descrise anterior se poate arata ca:C_d=

Obs. Cu cat nr simbolurilor de control e mai mare cu atat creste capacitatea de detectie.Capacitatea de corectie reprezinta raportul dintre numarul de secvente corectabile si numarul total de secvente posibile.Trebuie sa facem observatia ca in cazul codurilor bloc liniare numarul simbolurilor de control nu poate fi oricat de mare pt un numar dat de simboluri informatioale.

Limita poate fi exprimata mathematic astfel:

M_max=C_k¹+ . .+C_k^k=2^k-1