Reglarea automata a debitului

Reglarea automata a debitului

Un S.R.A. pentru debit are schema bloc din fig.1.1. Printr-o conducta de lungime L si diametru D curge un fluid cu debitul Q. Conducta e delimitata de elementul de executie EE si traductorul de debit TD. Pe baza informației primite de la traductorul de debit și a valorii prescrise Q₀, dispozitivul de reglare a debitului DRD da comanda spre elementul de execuție EE (un servoventil) pentru modificarea corespunzatoare a debitului Q.

Fig.1.1. S.R.A. pentru debit

Pentru reglarea debitului se determina modelul matematic al conductei tehnologice prin care curge un fluid. Se presupune curgerea prin conducta a unui lichid incompresibil (in cazul lichidului compresibil calculul fiind similar prin corectia cu un coeficient de compresibilitate) si se foloseste ecuația de conservare a impulsului care actioneaza in sistem pentru doua cazuri distincte, intalnite mai frecvent in practica :

conducte scurte cu ;

conducte lungi cu .

1.1.1. Modelul matematic al unei conducte scurte

Tronsonul de conducta se echivaleaza cu o rezistenta hidraulica pentru care este valabila relatia cunoscuta

unde :    Q - debitul de fluid ce trece prin conducta (Q_o in regimul stationar);

ΔP - caderea de presiune pe conducta (ΔP_o in regimul stationar);

- coeficient de debit;

S - sectiunea de trecere a fluidului;

- densitatea fluidului.

Pentru regim stationar de curgere se echilibreaza fortele care actioneaza

unde :    F_a - forta activa de apasare asupra lichidului din conducta

F_r - forta de reactiune pe tronsonul de conducta

Rezulta

In regim dinamic, diferenta dintre cele doua forte este compensata de viteza de variatie in timp a impulsului din sistem

unde M este masa de fluid din conducta si v este viteza de deplasare a fluidului.

Se obtine

Marimile care depind de timp se obtin daca se dau variatii arbitrare peste valorile de regim staționar

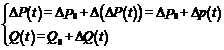(1.8)

Din (1.7) si (1.8) se obtine

și, extragand expresia regimului stationar si neglijand termenul patratic Q²(t), rezulta

Prin normare la valorile de regim stationar avem marimea reglata

si marimea de executie

rezultand modelul matematic temporal

(1.13)

unde V₀ este volumul de fluid in regim stationar in conducta.

Prin aplicarea transformatei Laplace, se obtine modelul matematic operational

(1.14)

unde :    T_pa - constanta de intarziere a conductei scurte

(1.15)

k_p - coeficientul de transfer al conductei k_p = 1/2.

Se obține astfel functia de transfer a conductei scurte

din care se observa ca o conducta scurta este un element aperiodic de ordinul intai.

1.1.2. Modelul matematic al unei conducte lungi

In acest caz se presupune ca forta de reactiune este forta de frecare a fluidului cu peretii conductei, debitul depinzand esential de lungimea L a conductei

(1.17)

unde k este coeficient de frecare al fluidului cu conducta.

Echilibrand fortele, pentru regimul stationar al procesului de curgere avem

(1.18)

Pentru regimul dinamic se poate scrie

(1.19)

Marimile variabile in timp au semnificatiile din (1.8) si atunci (1.19) devine

(1.20)

din care extragand expresia regimului stationar si neglijand termenul patratic ΔQ²(t)

(1.21)

Prin normare la valorile de regim stationar, ca in cazul precedent, se obtine modelul matematic temporal

(1.22)

Prin aplicarea transformatei Laplace, se obtine modelul matematic operational

(1.23)

unde :    T_pb - constanta de intarziere a conductei lungi

(1.24)

k_p - coeficientul de transfer al conductei k_p = 1/2.

Se obține astfel functia de transfer a conductei lungi

(1.25)

rezultand ca si conducta lunga este un element aperiodic de ordinul intai.

1.1.3. Proiectarea S.R.A. pentru debit

Consideram SRA din fig.1.1 la care cunoaștem functia de transfer a partii fixe

(1.26)

rezultata prin conectarea in serie dintre :

- traductorul de masura, considerat element proportional

- elementul de execuție, aproximat de un element aperiodic de ordinul intai

(1.28)

- procesul reglat, reprezentat de conducta tehnologica prin care circula debitul de fluid, cu functia de transfer determinata anterior :

(1.29)

Pentru automatizare se recomanda un regulator PI care asigura performante superioare in regim stationar. Intucat sistemele pentru reglarea debitului au inertii mici, frecventa cu care sunt scoase din regimul stationar este relativ mare, astfel ca este necesar un studiu asupra stabilitatii sistemului, din care vor rezulta concluzii utile proiectarii. Pentru analiza stabilitatii sistemului vom utiliza criteriul Nyquist-Neumark.

Functia de transfer a sistemului in circuit deschis este

(1.30)

de unde, aplicand transformata Fourier, se obtine

(1.31)

care poate fi descompusa in parte reala si parte imaginara

(1.32)

care da informatii despre locul de transfer a sistemului deshis.

Conditia ne da pulsatia la care locul de transfer taie axa imaginara

(1.33)

si conditia ne da pulsatia la care locul de transfer taie axa reala

(1.34)

Deoarece functia de transfer a sistemului deschis nu are poli in semiplanul drept, sistemul inchis e stabil daca locul de transfer al sistemului deschis nu inconjoara punctul critic de coordonate . In fig.1.2 sunt reprezentate cazurile :

locul de transfer a sistemului deschis nu taie axa reala dar taie axa imaginara (cazul a), deci nu exista pulsatie ω_R dar exista pulsatie ω_I;

locul de transfer a sistemului deschis nu taie axele reala si imaginara (cazul b), deci nu exista pulsatii ω_R si ω_I;

locul de transfer a sistemului deschis taie axa reala dar nu taie axa imaginara (cazul c), exista pulsatie ω_R si nu exista pulsatie ω_I.

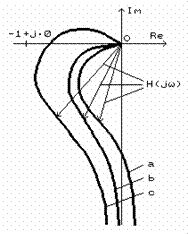
Fig.1.2. Locul de transfer a sistemului deschis

Primul caz e asigurat pentru orice valoare a factorului de amplificare k_R daca este indeplinita una din urmatoarele doua conditii

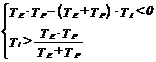(1.35)

Pentru a doua varianta este indeplinita conditia

cu restrictia de asigurare a stabilitatii (pentru constanta de timp T_i din (1.36) si _cr

Asadar, pentru ca sistemul sa fie stabil, sunt necesare conditii restrictive impuse parametrilor regulatorului (k_R si T_i). Se impune ca in proiectarea regulatorului sa se utilizeze o metoda bazata pe un criteriu integral in care sa se poata tine seama de restrictiile anterioare (1.36) și (1.37). Parametrii optimi de acordare ai regulatorului se determina prin rezolvarea problemei

(1.38)

sau a problemei

(1.39)

unde :    ε(t) - eroarea dinamica a sistemului;

- coeficient de ponderare a derivatei (t) fata de (t).

Criteriul integral J admite o exprimare directa, astfel incat problemele (1.38) sau (1.39) se reformuleaza astfel

(1.40)

respectiv

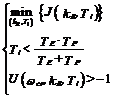(1.41)

Acestea sunt probleme de optimizare parametrica ce pot fi rezolvate prin metodele numerice, rezultand solutia (k_R^*,T_i^*).

Metoda propusa e avantajoasa si pentru ca poate lua in considerare si restrictii de ordin constructiv impuse de regulatorul fizic

(1.42)

1.1.4. Realizarea sistemelor pentru reglarea debitului

Sistemele pentru reglarea debitului sunt realizate in structuri simple de reglare dupa eroare ca in fig.1.1. O astfel de structura este folosita de sine statator pentru mentinerea unui debit la o valoare prescrisa, sau ca bucla secundara intr-o structura de reglare evoluata de cascada a debitului cu nivelul, temperatura, concentratia etc.

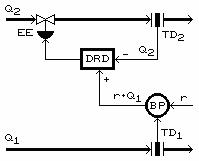
Fig.1.3. SRA de debit cu menținerea constanta unui raport dat intre doua debite

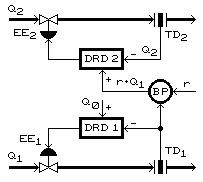
Fig.1.4. SRA de debit cu menținerea constanta unui raport dat intre doua debite și stabilizarea celuilalt debit

In unele aplicatii industriale se solicita mentinerea unui raport dat r intre doua debite Q₁ si Q₂. Aceasta cerinta este asigurata prin SRA avand schema bloc din fig.1.3, in care apare blocul de raport sau blocul proportional BP, care primeste la intrare o marime proportionala cu valoarea debitului Q₁ si la iesire genereaza marimea r·Q₁ care devine marime prescrisa pentru sistemul de reglare al debitului Q₂. In regimul de functionare al acestui sistem este satisfacuta relatia

(1.43)

In fig.1.4 se prezinta un sistem care realizeaza, pe langa mentinerea unui raport dat r intre doua debite Q₁ si Q₂, si stabilizarea debitului Q₁.