FORME DE REPREZENTARE A FUNCTIILOR LOGICE. MINIMIZAREA FUNCTIILOR LOGICE.

FORME DE REPREZENTARE A FUNCTIILOR LOGICE. MINIMIZAREA FUNCTIILOR LOGICE

ARGUMENT

Aparatura electronica moderna este realizata in proportie foarte mare cu circuite integrate digitale.

Exista o mare varietate de circuite integrate digitale care pot fi clasificate dupa mai multe criterii, dintre care cele mai importante sunt prezentate mai jos.

Dupa modul de functionare:

circuite logice combinationale;

circuite logice secventiale.

Dupa tipul tranzistoarelor utilizate :

circuite integrate cu tranzistoare bipolare;

circuite integrate cu tranzistoareunipolare.

Dupa gradul de complexitate :

circuite integrate pe scara mica (SSI);

circuite integrate pe scara medie (MSI);

circuite integrate pe scara mare (LSI);

circuite integrate pe scara foarte mare (VLSI).

Functiile realizate de circuitele integrate digitale se numesc functii logice. Pentru ele exista mai multe forme de reprezentare: tabelul de adevar, formele canonice, diagramele Veitch-Karnaugh. In functie de specificul aplicatiei este aleasa o forma de reprezentare sau alta.

Realizarea practica a unei functii logice cu circuite integrate digitale se numeste implementare. Implementarea este eficienta daca functia logica este adusa dintr-o anumita forma de reprezentare la forma cea mai simpla, numita si forma elementara. Procedeul prin care se obtine forma elementara se numeste minimizare.

CUPRINS

PARTEA I . FORME DE REPREZENTARE A FUNCTIILOR LOGICE

I.1. Definirea functiilor logice

Functia logica este o functie de n variabile cu proprietatea ca atat variabilele cat si functia nu pot lua decat valorile 0 sau 1.

Domeniul de definitie al unei functii logice de n variabile cuprinde 2ⁿ puncte, corespunzatoare tot atator combinatii distincte posibile care se pot realiza cu valorile variabilelor sale, care nu pot fi decat 0 sau 1.

Domeniul in care functia logica ia valori este format din multimea .

In expresia unei functii logice nu pot aparea decat suma logica, produsul logic si operatia de inversare (complementare).

Functii logice de baza de doua variabile

Pentru exprimarea unei functii logice se pot folosi diverse moduri de reprezentare.

Oricare ar fi forma de reprezentare, din ea trebuie sa rezulte ce valoare ia functia pentru toate punctele domeniului sau de definitie.

Alegerea unei anumite forme de exprimare a functiei logice este dictata in mare masura de natura aplicatiei.

I.2. Tabelul de adevar

Tabelul de adevar stabileste corespondenta dintre valoarea functiei si valorile variabilelor sale sub forma tabelara.

Pentru o functie logica de n variabile, numarul liniilor din tabel este 2ⁿ

A. Functii logice de doua variabile, f(A,B), reprezentate in tabel de adevar

Functia SI de doua variabile reprezentata in tabel de adevar

Functia SI ia valoarea 1 numai atunci cand toti termenii produsului sunt 1, iar daca cel putin un termen este 0, produsul va fi 0.

Functia SAU de doua variabile reprezentata in tabel de adevar

Functia SAU ia valoarea 0 numai atunci cand toti termenii sumei sunt 0, iar daca cel putin un termen este 1, suma va fi 1.

Functia SAU EXCLUSIV

Functia SAU EXCLUSIV ia valoarea 1 atunci cand variabilele ei au valori diferite.

Functia SAU EXCLUSIV se mai numeste si functie de anticoincidenta.

Functia SI NU de doua variabile reprezentata in tabel de adevar

Functia SI NU ia valoarea 1 daca cel putin un termen al produsului este 0, iar daca toti termenii sunt 1, functia ia valoarea 0.

Functia SAU NU de doua variabile reprezentata in tabel de adevar

Functia SAU NU ia valoarea 1 numai atunci cand toti termenii sumei sunt 0, iar daca cel putin un termen este 1, functia ia valoarea 0.

Functia SAU EXCLUSIV NEGAT

Functia SAU EXCLUSIV NEGAT ia valoarea 1 atunci cand variabilele ei au valori identice.

Functia SAU EXCLUSIV NEGAT se mai numeste si functie de coincidenta.

B. Functii logice de trei variabile, f(A,B,C), reprezentate in tabel de adevar

Tabelul de adevar pentru functiile de trei variabile, f(A, B, C), are 2³ = 8 linii.

Functia F(A, B, C), ia valoarea majoritatii variabilelor sale. De aceea ea se mai numeste " functie de vot majoritar ".

I.3. Forma canonica

Forma canonica este o reprezentare analitica a functiei logice care permite o examinare usoara a acesteia.

Exista doua moduri de scriere a unei functii logice in forma canonica :

ca o suma de termeni de tip produs numiti constituenti ai unitatii, ceea ce reprezinta forma canonica normala disjunctiva, prescurtat f.c.n.d.

ca un produs de termeni de tip suma numiti constituenti ai lui zero, ceea ce reprezinta forma canonica normala conjunctiva, prescurtat f.c.n.c.

In forma canonica normala disjunctiva expresia functiei contine termenii pentru care valoarea functiei este 1, iar in forma canonica normala conjunctiva apar termenii pentru care valoarea functiei este 0.

Exemplu

Forma canonica normala disjunctiva (f.c.n.d.) si forma canonica normala conjunctiva (f.c.n.c.) a functiei de " vot majoritar" F(A,B,C)

Forma canonica normala disjunctiva (f.c.n.d.) :

F = = P₃ + P₅ + P₆ + P₇

Forma canonica normala conjunctiva ( f.c.n.c.):

F = = S₀ * S₁ * S₂ * S₄

I.4. Diagrama Veitch-Karnaugh

Diagrama Veitch-Karnaugh este o reprezentare grafica a tuturor combinatiilor distincte posibile intre variabilele functiei. Ea poate fi privita ca reprezentarea grafica a formei canonice cu termeni minimali (f.c.n.d.).

Fiecare termen minimal este reprezentat printr-o celula, celulele fiind asezate astfel incat doua celule alaturate sa reprezinte termeni minimali ce difera prin valoarea unei singure variabile.

Ordinea termenilor minimali in diagrama Veitch-Karnaugh pentru functii de 2,3, respectiv 4 variabile

Termenul minimal reprezentat intr-o celula este determinat de valorile binare alocate variabilelor in celula respectiva, citite in urmatoarea ordine : mai intai valorile variabilelor scrise deasupra liniei diagonale (corespunzatoare celor mai mari puteri ale lui 2) si apoi valorile variabilelor scrise sub linie(corespunzatoare celor mai mici puteri ale lui 2).

Diagrama se construieste introducand un 1 in celulele care reprezinta termenii minimali din forma canonica normala disjunctiva a functiei si un 0 in restul celulelor.

Exemplu :

Functii de 3 si 4 variabile reprezentate in diagrame Veitch-Karnaugh

PARTEA A II -A. MINIMIZAREA FUNCTIILOR LOGICE

II.1. Generalitati

Minimizarea este procedeul de obtinere a formei elementare (minime, simplificate) pentru o functie logica data in forma neelementara.

Ea este absolut necesara in realizarea functiilor logice cu anumite tipuri de circuite, deoarece intre gradul de complexitate al functiei si cel al circuitului care o descrie exista o stransa legatura.

Minimizarea se poate realiza prin :

metoda analitica;

metoda diagramelor Veitch - Karnaugh.

Minimizarea prin metoda analitica se realizeaza prin aplicarea regulilor de calcul din algebra booleana, dar aceasta operatie este de obicei destul de dificila. Din acest motiv se prefera metoda diagramelor Veitch - Karnaugh.

II.2. Metoda diagramelor Veitch - Karnaugh

Prin aceasta metoda sunt aplicate regulile de calcul ale algebrei logice (distributivitatea si tertul exclus) pe reprezentarea functiei prin diagrame Karnaugh.

Termenii minimali din doua celule adiacente sunt identici cu exceptia unei singure variabile care intr-o celula apare complementata, iar in celula alaturata, necomplementata. Daca termenilor minimali din doua celule vecine li se aplica proprietatea de distributivitate si principiul tertului exclus , se elimina variabila care isi schimba valoarea. Pe diagrama Karnaugh acest lucru inseamna ca se scriu variabilele comune celor doua celule invecinate.

Exemplul 1

Gruparea celulelor care contin constituentii unitatii P₂ si P₃ ne conduce la expresia , iar gruparea celulelor vecine care contin constituentii unitatii P si P₆ conduce la expresia .

Forma minimizata a functiei rezulta prin scrierea sumei logice a celor doua expresii :

F = +

Daca grupul de doua celule vecine este vecin la randul sau cu un alt grup de doua celule vecine, acestea se pot uni intr-un grup de patru celule vecine, ceea ce permite eliminarea a doua variabile.

In general, un grup de 2ⁿ celule vecine ocupate de unitati permite eliminarea a n variabile.

Exemplul 2

In diagrama Veitch-Karnaugh corespunzatoare functiei

f = P₀ + P₁ + P₄ + P₅ + P₆ + P₇ + P₈ + P₉ + P₁₃ + P₁₅

se pot forma grupe de patru (2²) unitati, fapt care conduce la eliminarea a 2 variabile, din cele 4 ale functiei.

Gruparea celulelor care contin constituentii unitatii P₀, P₁, P₈ si P₉ conduce la expresia , gruparea celulelor vecine care contin constituentii unitatii P₄ , P₅ , P₆ si P₇ conduce la expresia , iar gruparii realizate cu P₅, P₇, P₁₃ si P₁₅ ii corespunde termenul BD.

Rezulta f = ++ BD

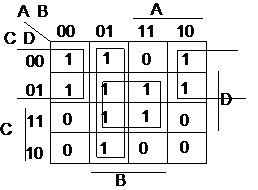
Fiecare celula ocupata cu unitati trebuie sa faca parte cel putin dintr-o grupare, dar poate fi inclusa si in mai multe grupari, daca acest lucru contribuie la o minimizare eficienta.

Simplificarea este maxima atunci cand unitatile din diagrama sunt incluse intr-un numar cat mai mic de grupari, fiecare dintre acestea continand un numar maxim de unitati.

Pentru a se aplica succesiv proprietatea de distributivitate si principiul tertului exclus, numarul unitatilor dintr-o grupa trebuie sa fie o putere intreaga a lui 2 (doua, patru sau opt unitati).

BIBLIOGRAFIE