Generarea (prelucrarea) prin aschiere

1.Stabilirea conditiilor tehnice si a caracteristicilor functionale

1.1.Tipuri de piese prelucrate

1.1.1. Forme geometrice ale suprafetelor componente. Conditii tehnice de prelucrare.

Fig.2

In constructia de masini productia are ca obiect fabricarea tuturor pieselor componente ale subansamblurilor si ansamblurilor functionale .Elementele de constructie care sta la baza oricarui subansamblu, impus de un anumit scop functional il constituie piesa.

Piesele sunt corpuri solide delimitate de suprafete aflate intr-o anumita combinatie si pozitie relativa, de anumite dimensiuni si calitate, toate impuse de rolul functional pe care il are piesa in ansamblul din care face parte.

Piesa fiind un corp solid este limitata de una sau mai multe suprafete componente distincte prin dimensiuni, forme si pozitii reciproce a caror totalitate determina suprafata piesei.

Fiecare din suprafetele componente ale pieselor se caracterizeaza:

printr-o forma geometrica (teoretica)

prin dimensiuni in diferite directii

printr-un anumit grad de netezime (rugozitate)

prin pozitia relativa a suprafetelor in ceea ce priveste paralelismul, perpendicularitatea, coaxialitatea, excentricitatea.

Toate acestea constituie conditiile tehnice de generare/executie a suprafetelor, prin care se determina forma, marimea pozitia si calitatea suprafetelor componente ale unei piese.

Aceste conditii tehnice si in primul rand forma geometrica sunt conditionate de functia pe care o va indeplini piesa in ansamblul din care va face parte. In constructia de masini piesele pot avea forme variate de la simple la complexe. Oricare ar fi piesa si forma sa ea este determinata de forma suprafetelor componente, acestea avand rol functional bine stabilit.

Suprafetele componente ale unei piese se pot prezenta sub diferite forme din punct de vedere geometric si sub diferite aspecte din punct de vedere tehnologic al rugozitatii acestora.

Forma si scopul functional al suprafetelor componente ale unei piese sunt importante in constructia de MU, pentru ca suprafata piesei nu poate fi obtinuta pe acelasi tip de MU, printr-un singur procedeu de generare (prelucrare), de aceea sunt necesare MU diferite pentru prelucrarea anumitor forme de suprafete (plane, cilindrice, elicoidale, evolventice).

Majoritatea pieselor din constructia de masini au ca suprafete componente suprafete geometrice simple: plane, cilindrice, conice, elicoidale, evolventice.

Conditiile tehnice de executie sunt:

conditiile de forma impun forma geometrica nominala pe care trebuie sa o aiba o suprafata reala si sunt si sunt stabilite prin abateri de forma admise de la forma geometrica a suprafetelor din care provin. Astfel de abateri sunt de: planeitate, cilindricitate, circularitate.

conditiile dimensionale stabilesc dimensiunile nominale ale suprafetelor reale si sunt date prin abaterile de la dimensiuni nominale, cum ar fi abateri de lungime, diametru, unghiular.

conditiile de pozitie relativa stabilesc distantele si orientarile relative nominale dintre suprafetele piesei sau fata de un alt reper impus sau convenabil ales. Aceste conditii sunt determinate prin abaterile de pozitie relativa cum sunt: abateri de paralelism, perpendicularitate, concentricitate.

conditii de calitate a suprafetelor - stabilesc calitatea necesara a suprafetelor reale pe care ea trebuie sa o aiba pentru indeplinirea rolului functional. Dintre aceste conditii importante sunt: rugozitatea, duritatea, tratamentele termice.

1.1.2. Realizarea curbelor generatoare si directoare

Din punct de vedere al realizarii tehnice, curbele generatoare pot fi materializate prin muchia aschietoare a sculei sau pot fi obtinute pe cale cinematica

Generatoarea materializata

In procesul de generare a suprafetelor pe masini - unelte, curba generatoare poate fi materializata prin forma muchiei aschietoare a sculei, adica programata pe scula, daca unghiul de degajare γ este nul, sau prin proiectia muchiei aschietoare pe planul generatoarei, cand unghiul γ are o valoare oarecare , diferita de zero.

In Fig.1 este exemplificat cazul ultim in care γ≠0; generatoarea G in planul sau Γ are o forma curba oarecare AMB,rezultand ca proiectie a muchiei aschietoare A'MB' a sculei.

Fig.3

In Fig.2 sunt exemplificate doua cazuri concrete de generare a unor suprafete prin strunjire (Fig.2,a) si prin rabotare (Fig.2,b) cu generatoare compuse din drepte si din arce de cerc, materializate prin muchia aschietoare a cutitului de strung si de raboteza.

Fig.4

Materializarea (programarea) generatoarei prin muchia aschietoare a sculei este posibila numai in cazurile in care lungimea acesteia nu este prea mare, deoarece cu cresterea lungimii muchiei aschietoare, apar probleme dificil de rezolvat din punct de vedere tehnic, in ceea ce priveste constructia sculei si intretinerea ei (reascutirea). Din aceste cauze, lungimea muchiei aschietoare a sculei, in general nu poate materializa lungimile generatoarelor folosite, in mare majoritatea a cazurilor, la generarea suprafetelor pe masini - unelte .

Solutia problemei consta in a recurge la utilizarea unei generatoare obtinuta pe cale cinematica.

Generatoarea cinematica

Generatoarea, fiind o curba, poate fi considerata din punct de vedere matematic, ca rezultand in mai multe moduri si anume ca:

urma unui punct K in deplasarea sa in plan;

infasurarea pozitiilor succesive ale unei curbe C care se deplaseaza intru-un plan;

intersectia a doua suprafete Σ₁ si Σ₂.

Primele doua cazuri de generare a unei curbe implica o miscare ce poate fi realizata prin intermediul unor elemente cinematice ale masinii - unelte cum sunt mecanismul fus-lagar si mecanismul ghidaj-sanie.

Generatoarea cinematica ca traiectorie a unui punct

Cea mai simpla dintre generatoarele cinematice, realizate ca traiectorie a unui punct este generatoarea rectilinie, in cazul strunjirii unei suprafete cilindrice (Fig.3,a).

Teoretic, se considera varful K al cutitului, ca fiind punctiform si dotat cu o miscare de translatie, de viteza v_k, pe o directie paralela cu axa piesei.

Trebuie de remarcat ca generatorea rectilinie nu mai este programata pe muchia aschietoare a sculei, ci pe elementele ghidaj-sanie apartinand masinii-unelte.

Generatoarele cinematice, cu forme mai complicate se obtin prin combinarea mai multor traiectorii rectilinii si circulare, realizate de mecanismele masinii-unelte.

Fig.5

Directoarea cinematica

In procesul de generare a suprafetelor reale pe masinile-unelte se intalnesc trei cazuri de realizare a directoarei cinematice : ca traiectorie a unui punct , ca infasuratoare a unei curbe cinematice , prin transpunere (imprimare) prin rulare .

a . Directoarea cinematica ca traiectorie a unui punct.

Traiectoria directoare circulara D (fig.4 , a) se poate considera ca rezultand prin deplasarea punctului M in jurul axei de rotatie , la distanta R_M si cu turatia n_as,avand deci viteza tangentiala v_M .

Generarea suprafetei implica deplasarea generatoarei pe traiectoria directoare , deci existenta unei viteze v_M a carei marime si sens nu sunt impuse , putind avea orice valori (diferite de zero) .De asemenea , miscarea pe traiectoria directoare ,rectilinie sau circulara , poate fi continua sau nu , fara a influenta forma ei .

Aceste proprietati ale generarii traiectoriei directoare permit ca viteza de deplasare v_M a unui punct al generatoarei pe directoare , sa poata fi aleasa in concordanta cu cerintele tehnologice ale procesului de aschiere , si anume ca marime a vitezei de aschiere .

Fig.6

Privind tipul miscarii principale si directia vitezei principale de aschiere v_as cu care se efectueaza , se disting doua cazuri :

1. La generarea suprafetelor reale , la care directoaera D se realizeaza ca traiectorie a unei miscari simple , de rotatie sau de translatie , viteza principala de aschiere este viteza elementului generator in lungul traiectoriei directoare si , implicit , miscarea principala o reprezinta acea miscare simpla.

Este cazul generarii suprafetelor reale prin mai multe procedee de generare prin aschiere , de exemplu , prin strunjire (fig.5,a) sau rabotare (fig.5,b).

2. In cazurile de generare , in care directoarea teoretica D se realizeaza ca traiectorie (sau arce de traiectorie ) a unei miscari rezultante obtinute din compunerea mai multor miscari simple , de rotatie sau de translatie viteza principala de aschiere este viteza elementului generator in lungul celei mai apropiate traiectorii componente a traiectoriei directoare .

Rezulta astfel ca miscarea principala o reprezinta acea miscare simpla avand aceasta traiectorie componenta .

Generarile de acest fel , considerate particulare cazului general , sunt specifice frezarii si rectificarii suprafetelor reale , strunjirii filetelor etc.

De exemplu , la frezarea unei suprafete plane (fig.5,c) , directoarea teoretica D se realizeaza ca infasuratoare a unei curbe cinematice , adica a directoarei elementare D_E , ce reprezinta un arc al directoarei reale , D_real . Cum aceasta din urma este traiectoria miscarii rezultantei dintre miscarea de rotatie a frezei , n_as si miscarii de avans relativ al frezei fata de semifabricat , v_sL , miscare rezultanta denumita mai sus , miscare de aschiere , rezulta ca traiectoria D_real se confunda cu traiectoria miscarii de aschiere ,Tr_as .

Ori , tangenta la traiectoria Tr_as (D_real) este viteza reala de aschiere , v_ras , si in consecinta , viteza principala de aschiere v_as va fi viteza tangenta la traiectoria circulara , cea mai apropiata traiectorie componenta a directoarei reale , D_real .

Rezulta astfel ca miscarea principala este data de miscarea de rotatie a frezei , a carei traiectorie circulara se parcurge cu viteza principala de aschiere , v_as .

In baza aceluiasi rationament , la rectificarea suprafetelor reale , miscarea principala o constituie miscarea de rotatie a pietrei de rectificat .

In cazul strunjirii filetelor (fig.5,d) , directoarea suprafetei elicoidale a acestora este elicea cilindrica D . Pentru realizarea sa cinematica , se compune miscarea de rotatie a piesei , n_as , care asigura pe traiectoria circulara viteza tangentiala v_T , cu miscarea rectilinie de deplasare axiala a cutitului , v_A , astfel incat sa existe intre ele o coordonare cinematica pentru a se obtine traiectoria directoare elicoidala D , de pas p si unghi β cunoscute .

Miscarea rezultanta a acestor miscari componente este miscarea de aschiere si deci , traiectoria directoare D fiind tocmai traiectoria miscarii de aschiere Tr_as , viteza reala de aschiere va fi tangenta la traiectoria directoare D .

fig.7

1.1.3.Generalitati despre generarea (prelucrarea) prin aschiere

In orice generare prin aschiere , semifabricatul contine adaosul de prelucrare a carui marime influenteaza productivitatea procedeului la generarea suprafetelor pe masinile-unelte. Marimea adaosului de prelucrare depinde de : materialul semifabricatului si procedeul tehnologic de obtinere a sa , dimensiunile , greutatea si complexitatea formei piesei finite , precizia dimensionala , de netezime si a pozitiilor relative prescrise suprafetelor prelucrate ale piesei finite , caracterul productiei de realizare a piesei finite (individuala , serie mica , mijlogie sau masa).

Adaosul de prelucrare este variabil de la o generare la alta , putand fi mai mare sau mai mic.Ca urmare , in miscarea relativa dintre taisul sculei aschietoare si adaosul de prelucrare , acesta poate fi indepartat in intregime dintr-o data , adica intr-o singura etapa daca este mic , sau in mai multe etape , daca adaosul este mare.

Divizarea adaosului de prelucrare in straturi partiale si in straturi de aschiere se poate considera in urmatoarele moduri :

Divizarea in sensul adancimii adaosului.

In figurile 2,a si b, reprezentand strunjiri cu cutite profilate , divizarea are loc numai in sensul adincimii A a adaosului de prelucrare , in care scop scula cuprinde intreaga latime a suprafetei prelucrate si se deplaseaza numai in sensul adincimii adaosului printr-o miscare de avans transversal , v_sT. Se poate observa ca in aceste cazuri straturile de aschiere au latimi mari si forme identice cu ale taisului sculei .

Divizarea in sensul latimii adaosului .

In figura 2,c, reprezentand procedeul de strunjire a unei piese cilindrice , divizarea are loc numai in sensul latimii adaosului , straturile de aschiere fiind indepartate printr-o miscare de avans longitudinal v_sL efectuata in sensul latimii adaosului. Divizarea se aplica atunci cand taisul sculei nu poate cuprinde intreaga latime a adaosului .

Divizarea in sensul lungimii adaosului .

In figura 2,d, unde este reprezentata schema de generare a unei suprafete plane prin procedeul de frezare , divizarea are loc in sensul lungimii adaosului. Pentru indepartarea straturilor de aschiere piesa-semifabricat executa o miscare de avans director v_sU , in sensul lungimii adaosului.

Divizarea mixta

Este o combinatie a diferitelor moduri de divizare prezentate si se aplica atunci cind adaosul de prelucrare trebuie indepartat in mai multe treceri. In figura 2,e, este ilustrat un asemenea exemplu de divizare mixta , in sensul adincimii si latimii adaosului de prelucrare , in cazul strunjirii unei piese cilindrice.

Fig.8

In cazul cel mai general de generare a suprafetelor prin aschiere pe masini-unelte , miscarea relativa dintre taisul sculei aschietoare si piesa semifabricat , necesara indepartarii adaosului de prelucrare , este o rezultanta a unor miscari simple , de rotatie si translatie pe care le poate executa simultan atat scula cat si piesa-semifabricat.

Fiecare procedeu de generare prin aschiere impunand ce miscari trebuie sa existe la generarea suprafetei in cauza , conduce la stabilirea cinematicii masinii-unelte pe care sa se execute generarea respectiva. Cu alte cuvinte , fiecare procedeu de generare (prelucrare) prin aschiere conduce , din punct de vedere al cinematicii , la un anumit tip distinct de masina-unealta.

1.1.4 Particularitati ale procesului de aschiere

La prelucrarile cu sculele de strunjit interior si de canelare (retezare), datorita volumului redus al partii active a acestora, efectul de uzura al sculelor este mai pronuntat. La fel la prelucrarile frontale, unde exista variatii mari ale vitezei de aschiere in lungul razei semifabricatuluui prelucrat, modul de comportare al sculei este diferit scula uzandu-se mai rapid in primele momente de lucru, in zona vitezelor mari de aschiere.

Criteriul de uzura utilizat, in exploatarea cutitelor de strung este uzura fetei de asezare - criteriul h_α [mm]. La strunjire, rugozitatea de generare a suprafetei, se calculeaza cu relatiile:

in care: r_ε este raza varfului sculei; χ si χ₁ - unghiurile de atac, principal si secundar.

La strunjirea de finisare, datorita razei de ascutire a taisului ρ_β, scula va detasa aschia numai pana la o grosime minima, a_min, fig.7. Restul de material, nemaiputand fi detasat, va suferi o deformare plastica importanta, se va ecruisa si refula pe sub tais, va genera asperitatea.

Fig.9

Daca se considera o anumita grosime a aschiei a_x, pentru o anumita adancime t_x, se poate scrie:

1. Regimul de aschiere la strunjire

La stabilirea marimii valorilor parametrilor regimului de aschiere, t, s, v_as trebuie avute in vedere: forma si dimensiunile semifabricatului, precizia si rugozitatea suprafetei prelucrate, caracteristicile mecanice si starea suprafetei materialului prelucrat, materialul, constructia si parametrii geometrici ai sculei, conditiile in care se desfasoara procesul de aschiere (racire, ungere) etc. Cresterea productivitatii operatiei la strunjirea de degrosare este mai rational sa se obtina prin marirea sectiunii de aschiere decat prin marirea vitezei de aschiere.

Marirea avansului depinde de rezistenta corpului sculei, a placutei de carbura metalica, a mecanismelor de avans ale caruciorului, momentul de torsiune admis de mecanismul miscarii principale, de rigiditatea elementelor sistemului tehnologic.

Viteza tehnologica de aschiere la strunjirea longitudinala se calculeaza cu relatia:

in care : T - durabilitatea sculei, [minute],

m - exponentul durabilitatii

C_v, x_v, z_v - coeficient si exponenti depinzand de caracteristicile materialului prelucrat

HB - duritatea materialului prelucrat, pentru otel carbon cu HB≤130 exponentul n este egal cu unu, pentru otel carbon cu HB>130, n=1,75;

K - produs de coeficienti de corectie

Se calculeaza turatia axului principal al strungului cu relatia

,

in care : v_thas- viteza tehnologica de aschiere [m/min]

D- diametrul semifabricatului [mm]

Se adopta o turatie din gama de turatii posibile de realizat de catre axul principal al masinii-unelte n_mas, imediat interioara turatiei calculate n_as n_mas≤n_as

b.Fortele de aschiere la strunjire

Componentele fortei de aschiere la strunjire F_x, F_y, F_z se calculeaza cu relatiile politropice:

in care coeficientii C_Fx, C_Fy, C_Fz si exponentii x_Fx..C_Fz sunt dati in tabele.

Coeficientii de corectie K_Fx, K_Fy, K_Fz sunt produsul a sase coeficienti de corectie partiali.

Puterea necesara aschierii este data de relatia:

Fig.10

2. Proiectarea cinematica si organologica

2.1.Analiza constructiva

2.1.1. Analiza caracteristicilor tehnice si economice ale unor masini de lucru

CARACTERISTICILE TEHNICE FUNCTIILE PRINCIPALE

CARACTERISTICILE TEHNICE FUNCTIILE PRINCIPALE

CARACTERISTICILE TEHNICE FUNCTIILE PRINCIPALE

LODGE & SHIPLEY Strung pentru prelucrarea suprafetelor sferice  -  w/Construit-In masa rotativa

2.1.2. Schema bloc a masinii de lucru

1,2,3 - manete pentru setarea numarului de turatii al strungului

4- maneta pentru schimbarea de la viteza normala la viteza mare

5- maneta pentru schimbarea de la filetare pe dreapta la filetare pe stanga

6- maneta pentru setarea vitezei de avans si filet

7- maneta pentru multiplicarea avansului (butuc interior) respectiv pentru cuplarea surubului de avans sau avansul vergelei (butuc exterior).

8,15- maneta pentru pornirea, oprirea si schimbarea sensului de miscare transfer la arborele principal

9- roata de mana pentru deplasarea manuala a saniei

10- maneta pentru controlul manual al avansului transversal

11- maneta pentru deplasarea postului culisant al sculei

12- buton pentru cuplare si decuplare a mecanismului de siguranta

13- buton pentru setarea decuplarii la incarcare

14- maneta pentru cuplarea piulitei surubului conducator

16- buton pentru controlul rapid al avansului transversal si longitudinal

17- maneta pentru saniei si mutarile culisante transversale

18- maneta pentru strunjire si strangerea suportului sculei

19- maneta pentru blocarea pinolei

20- maneta pentru blocarea rapida a pinolei in directie gresita

21- roata de mana pentru actionarea mansonului pinolei

22- comutarea fusului

23- comutarea iluminarii

24- comutarea pompei de racire

25- comutarea controlului de departe al motorului de actionare

2.2. Proiectarea cinematica si organologica

2.2.1. Analiza cinematica a unor masini de lucru similare

Schema cinematica a strungului SN40

Schema cinematica a strungului 1M 620

Schema cinematica a strungului 1A 616

Schema cinematica a strungului DLZ 315

Schema cinematica a strungului DU 40

Schema cinematica a strungului C 11A

2.2.2. Proiectarea cinematica si organologica a lantului cinematic principal

2.2.2.1. Alegerea motorului de actionare a lantului cinematic

Viteza tehnologica de aschiere la strunjirea longitudinala se calculeaza cu relatia:

in care:

T- durabilitatea sculei [min]

m- exponentul durabilitatii

C_v, x_v, y_v- coeficient si exponenti depizand de caracteristicile materialului

prelucrat

HB- duritatea materialului prelucrat

Pt. Otel carbon HB ≤ 130, n = 1

Pt. Otel carbon cu HB > 130, n = 1,75

K- produs de coeficienti de corectie

Fortele de aschiere la strunjire:

Puterea necesara aschierii este data de relatia:

2.2.2.2. Calculul cinematic al lantului cinematic principal

Se cunosc:

- numarul de trepte de turatii ale mecanismului de reglare

q = 9

- ratia seriei geometrice a marimilor de iesire

φ = 1,25

- marimea minima de iesire

n_min = 40 rot/min

1. Alegerea valorilor turatiilor

n₁ =40 rot/min              n₆ =125 rot/min

n₂ =50 rot/min n₇ =160 rot/min

n₃ =63 rot/min n₈ =200 rot/min

n₄ =80 rot/min n₉ =250 rot/min

n₅ =100 rot/min                        

2. Stabilirea ecuatiei structurale

Ecuatia structurala se stabileste in baza numarului de trepte de turatii q = 10 ale mecanismului de reglare.

Ecuatia structurala a mecanismului de reglare fiind de forma unui produs de factori se bucura de proprietatea de comutativitate.

Ca urmare, acestei ecuatii ii corespunde un numar N ' de ecuatii structurale obtinute prin permutarea factorilor

N' = k ! / ( l! m! n!)

unde k reprezinta numarul de termeni ai ecuatiei structurale, iar l, m, n, numarul de factori identici ai aceleiasi ecuatii.

Numarul q al treptelor de turatii obtinute la ultimul arbore K, dispuse in serie geometrica cu ratia φ, are indicele 1 si, ca urmare, in partea din dreapta a ecuatiei exista unul si numai unul dintre factori (oricare dintre acestia) care are acelasi indice 1.

Dupa marcarea indicelui 1 unuia dintre factori, indicii celorlalti factori se obtin prin regula de formare a indicilor. Conform acesteia, urmatorul indice pentru oricare din factori se obtine ca produs intre indicele 1 si factorul acestuia. In continuare se procedeaza similar cu noul indice obtinut.

Ca urmare a aplicarii regulii de formare a indicilor, numarul de ecuatii structurale ale retelei de turatii devine

N = N' k! = (k!)² / (l! m! n!)

Se considera ecuatia structurala a mecanismului de reglare 9 = 3 x 3, careia ii corespunde un numar de N = (2!)² / 2! = 2 ecuatii structurale ale retelei de turatii. Acestea se obtin procedand astfel :

9 = 3₁ x 3₃

9 = 3₃ x 3₁

Ecuatia structurala a mecanismului de reglare aleasa este 

9 = 3₃ x 3₁

3. Alegerea retelei structurale optime

Reteaua structurala optima trebuie sa respecte:

Criteriul functional pentru lantul cinematic principal conform caruia, rapoartele de transmitere ale angrenajului, care satisfac in mare masura cerintele de rezistenta la uzura si oboseala, zgomot minim si randament maxim au valorile :

i_Rmax ≤ 2 sii_Rmin ≥ 1/4

Criteriul de rezistenta doar pentru arborele intermediar, impune ca in interiorul mecanismului de reglare arborii sa fie supusi concomitent la cele mai mici solicitari, avandu-se in vedere obtinerea unor arbori de diametru cat mai mic. Acest criteriu este indeplinit cel mai bine de retelele structurale intretesute, la care atat indicii cat si factorii cresc de la dreapta spre stanga.

Fig.11

Pentru arborele I avem trei turatii la distanta de 1 φ.

Intre arborele I si II avem cate trei turatii la distanta de 3 φ.

4. Realizarea schemei cinematice

Fig.12

5. Elaborarea diagramei de turatii.

In aceasta etapa de proiectare se cunosc : ratia φ = 1,25 ; numarul de trepte q =9 ; domeniul de turatii ale ultimului arbore al mecanismului de reglare (D_n = n_min . n_max), reteaua structurala optima, turatia (turatiile) in sarcina a motorului electric (n_ME = 1450 [rot/min]).

Pentru reprezentarea diagramei de turatii se recomanda :

evitarea raportului 1/1 si a rapoartelor de transfer limita i_Rmax ≤ 2 = φ^a si, mai ales, i_Rmin ≥ ¼ = 1/φ^b ;

adoptarea unor rapoarte de transfer de multiplicare si de demultiplicare, crescatoare de la iesire spre intrare.

Fig.13

6. Calculul numarului de dinti ai rotilor pentru angrenaje.

Din conditii de gabarit, la masinile-unelte, suma numerelor de dinti pentru angrenajele dintre doi arbori ai mecanismului de reglare este constanta fiind limitata la valoarea Σz ≤ 120.

6.1. Determinarea rapoartelor de transmitere

Determinarea rapoartelor se face pa baza diagramei de turatii construita la punctul anterior. Astfel vom avea:

n₀ = n₁₀ = 250 [rot/min]

n_ME =1450 [rot/min]

i₁ - raportul de demultiplicare al transmisiei cu curea ;

i_R1. i_R7 - raportul de transmitere.

6.2. Determinarea numarului de dinti

Treapta I - pentru angrenajele ce transmit miscarea de la arborele 0 la arborele I:

M_min = cel mai mic multiplu comun al sumelor (A­_k+B_k) ;

Q_­min= factor, si se calculeaza cu relatia :

unde z'_k = numar intreg, are valoarea minima de 17 dinti, z'_k≥17.

Observatie: in urma calcularii lui Q_min se alege numar intreg mai mare sau egal cu cel obtinut prin calculare.

Σz = suma minima a numarului de dinti ale angrenajului dintre doi arbori

Σz = M_min · Q_min

Σz_I = M_minI · Q_minI = 42 · 2 = 84

z'_k, z''­_k = numarul de dinti ai rotii dintate conducatoare /conduse si se calculeaza cu relatiile :

Tinand seama de aceste relatii vom avea :

Treapta a II - a - pentru angrenajele ce transmit miscarea de la arborele I la arborele II:

Σz_II = M_minII · Q_minII = 42 · 2 = 84

7. Recalcularea turatiilor.

Recalcularea turatiilor se face pe baza diagramei de turatii:

In continuare se va calcula eroarea Δn. Pentru lantul cinematic principal trebuie sa se regaseasca in intervalul -2 ≤ Δn ≤ 3

Fig.14

Alegem un motor electric asincron tip 112M Bucuresti STAS 881-88 cu urmatoarele caracteristici tehnice :

turatia de mers in gol de 1500 rot/min

puterea electrica activa de 4 KW

turatia efectiva de 1425 rot/min

dimensiunile de gabarit sunt prezentate in plansa 01

Plansa 01

2.2.2.3 Calculul transmisiei prin curele trapezoidale

Se cunosc : - puterea de transmis 7 KW

- turatia rotii conducatoare 1425 rot/min

- raportul de transfer i₁₂=1,7

Alegem o curea tip SPA cu urmatoarele caracteristici conform STAS 7192-83

l_pּh = 8,5 x 8,0

h±Δh=8±0,4 mm    A_C=84 mm²

b_max=2,0 mm                        Alegem D_p1=90 mm conform STAS 1163-71

α=40˚±1˚

L_pmin=630 mm

L_pmax=3550 mm

D_pmin=71 mm

v    calculul diametrului primitiv al rotii conduse D_p2

D_p2= (1 - ξ)ּD_p1ּi_TC

in care :

ξ- este alunecarea elasticaξ=2%

D_p2= (1 - 0,02)ּ90ּ1,7

D_p2=149,94 mm

Se alege : D_p2= 160 mm

v    Calculul vitezei periferice

v    Alegerea distantei axiale

0,7(D_p1+D_p2)≤A₁₂≤2(D_p1+D_p2)

0,7(90+160)≤A₁₂≤2(90+160)

175≤A₁₂≤500

Se alege : A₁₂= 400 mm

v    Calculul lungimii primitive orientative a curelei

Se alege : L_porientativ= 1250 mm

v    Recalcularea distantei intre axe :

in care : γ este unghiul ramurilor curelei

β - unghiul de infasuratoare pe roata conducatoare

β₁=180 - γ ; β₁=169,9604˚= 2,6697 rad

β₂=180 + γ ; β₂=190,0396˚= 2,9851 rad

v    Calculul preliminar al numarului de curele

in care :

P - puterea pe arborele rotii conducatoare

P= 7KW

c_f - coeficientul de functionare c_f =1,7

c_L - coeficientul de lungime a cureleic_L= 0,94

c_β - coeficientul de infasurare al curelei pe roata mica (roata conducatoare)

c_β = 1 - 0,003 (180⁰ - β₁)

β₁ - unghiul de infasurare pe roata conducatoare in grade ;

c_β= 1 - 0,003 (180⁰ - 169,9604⁰) ; c_β= 0,9698

P₀ - puterea transmisa de o curea [KW]

Se alege conform STAS 1163 - 71

P₀ = 1,8 KW

v    Calculul numarului final de curele

in care : C_z este coeficient care tine seama ca momentul de torsiune nu se repartizeaza uniform pe cele doua curele z₀

C_z= 0,90 z=7/0,90 ; z= 7,77 ≈7 curele

v    Verificarea frecventei indoirilor

in care : x - numarul de roti de curea ale transmisiei

f_a - frecventa maxima admisa ; f_a = 80Hz

v    Forta de intindere initiala (F₀) si a apasarii pe arbori (F_a)

F₀ = (1,5..2)F_u F_u = 1000ּP/v₁

F_a = (1,5..2)F_u F_u = 1000ּ4/6,71 ; F_u = 596,12 daN

F₀ = (894,18...1192,24) daN

F_a = (894,18...1192,24) daN

2.2.2.4.Calculul angrenajelor

Alegerea materialelor pentru rotile dintate si a tratamentelor termice.

Se alege un aliaj 21MoMnCr 12 STAS 791 - 80, cu urmatoarele caracteristici : Toate pinioanele sunt durificate superficial prin cementare (Ce),nitrocementare (Nce)

1. Duritate a) flanc : 56 - 57 HRC

b) miez : 250 HB

2. Rezistenta la pitting σ_Hlim

1240 MPa

3. Rezistenta la piciorul dintelui σ_Flim

300 N/mm²

4. Rezistenta la rupere R_m (σ_r).

1080 N/mm²

5. Limita de curgere σ_p0,2(σ_c)

835 N­/mm²

I. Calcul cinematic

Calculul momentelor de torsiune si a puterii pe fiecare arbore .

P₀ = 7 KW ; P₁ = P₀ ּη_TCTּη_C

P₁ = 7ּ0,95ּ0,99 = 6,583 KW

η_TCT = 0,94..0,95 - randamentul transmisiei prin curele trapezoidale

η_r = 0,99..0,95 - randamentul rulmentilor

η_r.d.cil. = 0,97..0,99 - randamentul unui angrenaj cu roti dintate cilindrice

P₂ = P₁ּη_r.d.cil.ּη_r = 6,583ּ0,95ּ0,99 = 6,19 KW

P₃ = P₂ּη_r.d.cil.η_r = 6,19ּ0,95ּ0,99 = 5,82 KW

Calculul turatiilor

n₀ = 1425 rot/min
i₀₁=0,17n₁ = n₀ּi₀₁ = 242,25 rot/min

i₁₂= 0,35 n₂ = n₁ּi₁₂ = 84,78 rot/min

i₂₃=0,71n₃ = n₂ּi₂₃ = 60,19 rot/min

Calculul momentelor de torsiune

M_t = 955ּ10⁴ּP/n

M_t1 = 955ּ10⁴ּP₁/n₁

M_t1 = 955ּ10⁴ּ6,583/ 242,25 = 259515.5 Nmm

M_t2 = 955ּ10⁴ּP₂/n₂

M_t2 = 955ּ10⁴ּ6,19/84,78 =697269,40 Nmm

M_t3 = 955ּ10⁴ּP₃/n₃

M_t3 = 955ּ10⁴ּ5,82/60,19 = 923425,81 Nmm

Determinarea elementelor dimensionale principale ale angrenajului cilindric exterior cu dinti drepti

A. Distanta dintre axe a₁₂

Distanta minima dintre axe se determina din conditia ca dantura sa reziste la oboseala la presiune hertziana de contact (pitting)

K_H - factorul global al presiunii hertziene de contact

K_H = 105000 N/mm²

K_A - factorul de utilizare;K_A = 1,25

M_tp - momentul de torsiune pe arborele pinionului in Nּmm

M_tp = 259515.5 Nּmm

Ψ_d = b/d₁ - raportul dintre latimea danturii si diametrul de divizare al pinionului

Ψ_d = 0,4

σ_Hlim - rezistenta la pitting , presiunea hertziana limita la oboseala [N/mm²]

σ_Hlim =1240 N­/mm²

u - raportul nr. de dinti

Se alege conform STAS :a_min01 = 80 mm

a_min12 = 88 mm

B. Modulul danturii rotilor dintate

Modulul minim al danturii rotilor dintate care formeaza angrenajul se determina din conditia ca dantura rotilor dintate sa reziste la rupere prin oboseala la piciorul dintelui .

K_F - factorul global al tensiunii de la piciorul dintelui ; K_F = 1,7

K_A - factorul de utilizare ; K_A = 1,25

M_tp - momentul de torsiune pe arborele pinionului ; M_tp = 259515.5 Nmm

Ψ_d - raportul dintre latimea danturii si diametrul de divizare al pinionului

Ψ_d = 0,4

A₀₁ - distanta dintre axe

σ_Flim - rezistenta limita de rupere prin oboseala la piciorul dintelui   σ_Flim = 300 N/mm²

Se alege conform STAS : m_min01 = 2 mm

m_min12 = 2 mm

D. Calculul distantei de referinta intre axe

Distanta de referinta intre axe (distanta dintre axe in cazul in care angrenajul ar fi nedeplasat ) este data de relatia :

II. Calculul geometric al angrenajelor cilindrice exterioare cu dinti drepti

A. Elementele cremalierei de referinta

Daca generarea danturii se face cu freza melc se obtin la dantura rotii elementele cremalierei de referinta , care sunt standardizate prin STAS 821 - 82 .

Fig.15

α₀ = 20^o - unghiul profilului de referinta ;

h_oa^* = 1 - coeficientul inlatimii capului de referinta ;

h_of^* = 1,25 - coeficientul inaltimii piciorului de referinta ;

c_o^* = 0,25 - jocul de referinta la picior ;

c^*_{o max} = 0,35 - daca generarea danturii se face cu roata generatoare .

B. Calculul coeficientilor deplasarilor specifice ale danturii

- Unghiul de rostogolire

- Suma coeficientilor deplasarilor specifice ale danturii rotilor

C. Elementele geometrice ale angrenajului

- Diametrele de divizare D_d = mּz [mm]

D_d1 = 48 mm ; D_d2 = 120 mm ;D_d3 = 56 mm ;

D_d4 = 112 mm ; D_d5 = 70 mm ;D_d6 = 98 mm ;

D_d7 = 48 mm ;D_d8 = 120 mm ; D_d9 = 74 mm ;

D_d10 = 94 mm ; D_d11 = 98 mm D_d12 = 70 mm ;

- Diametrele de baza D_b = D_dּcosα [mm]

D_b1 = 45 mm ; D_b2 = 113 mm ;D_b3 = 53 mm ;

D_b4 = 105 mm ; D_b5 = 66 mm ;D_b6 = 92 mm ;

D_b7 = 45 mm ;D_b8 = 113 mm ; D_b9 = 70 mm ;

D_b10 = 88 mm ; D_b11 = 92 mm D_b12 = 65 mm ;

- Diametrele de rostogolire

D_w1 = 46 mm ; D_w2 = 115 mm ;D_w3 = 53 mm ;

D_w4 = 107 mm ; D_w5 = 67 mm ;D_w6 = 94 mm ;

D_w7 = 50 mm ;D_w8 = 125 mm ; D_w9 = 77 mm ;

D_w10 = 98 mm ; D_w11 = 102 mm D_w12 = 73 mm ;

- Diametrele de picior D_f = D_d - 2m(h^*_of - x₁₂) [mm]

D_f1 = 49 mm ; D_f2 = 127 mm ;D_f3 = 58 mm ;

D_f4 = 118 mm ; D_f5 = 67 mm ;D_f6 = 93 mm ;

D_f7 = 44 mm ;D_f8 = 111 mm ; D_f9 = 69 mm ;

D_f10 = 90 mm ; D_f11 = 94 mm D_f12 = 66 mm ;

- Diametrele de cap D_a = D_d +2m(h^*_oa + x) [mm]

D_a1 = 58 mm ; D_a2 = 136 mm ;D_a3 = 67 mm ;

D_a4 = 128 mm ; D_a5 = 76 mm ;D_a6 = 102 mm ;

D_a7 = 53 mm ;D_a8 = 125 mm ; D_a9 = 79 mm ;

D_a10 = 99 mm ; D_a11 = 103 mm D_a12 = 73 mm ;

- Calculam jocurile la picior

C₁ = 26,5ּm ≥ 0,1ּm ; C₂ = 21,5 ≥ 0,1ּm ; C₃ = 13,8 ≥ 0,1ּm ;

C₄ = 16,17 ≥ 0,1 ּm ; C₅ = 29,2 ≥ 0,1ּm; C₆ = 14,3 ≥ 0,1ּm ;

- Inaltimea dintilor

h₁ = 4.5 mm ; h₂ = 4,5 mm ; h₃ = 4,5 ; h₄ = 5 ; h₅ = 4,5; h₆ = 4,5; h₇ = 4,5

h₈ = 7 ; h₉ = 5 ; h₁₀ = 4,5; h₁₁ = 4,5; h₁₂ = 3,5

- Unghiul de presiune la capul dintelui

α_a1 = 38,95 ; α_a2 = 33,98 ;α_a3 = 38,24 ; α_a4 = 34,69 ; α_a5 = 30,05

α_a6 = 25,46 ; α_a7 = 31,67 ;α_a8 = 25,56 ; α_a9 = 28,33 ; α_a10 = 26,84

α_a11 = 26,60 ; α_a12 = 25,70

- Arcul dintelui pe cercul de cap

invα_a = tgα_a - α^o/180^o ּ π

invα_a1 = 0,459 ; invα_a2 = 0,324 ; invα_a3 = 0,438 ; invα_a4 = 0,343 ;

invα_a5 = 0,229 ; invα_a6 = 0,127 ; invα_a7 = 0,267 ; invα_a8 = 0,129 ;

invα_a9 = 0,190 ; invα_a10 = 0,156 ; invα_a11 = 0,151; invα_a12 = 0,132

S_a1 = 2,055 ; S_a2 = 1,980 ; S_a3 = 2,933 ; S_a4 = 1,023 ; S_a5 = 1,917

S_a6 = 2,488 ; S_a7 = 1,954 ; S_a8 = 1,122 ; S_a9 = 1,923 ; S_a10 = 2,158

S_a11 = 2,559 ; S_a12 = 1,964

- Latimea danturii rotilor

Pentru compensarea erorilor de montaj axial latimea pinionului se adopta mai mare decat latimea rotilor.

b₂ = 19.2 mm ; b₄ = 44.8 mm ; b₅ = 44.2 mm ; b₇ = 53 mm ; b₉ = 42.6 mm

b₁ = 24.2 mm ; b₃ = 49.8 mm ; b₆ = 39.2 mm ; b₈ = 48 mm ; b₁₀ = 37.6 mm

b₁₁ = 33 mm ; b₁₂ = 28 mm

Gradul de acoperire

ε_α12 = 2,70 ; ε_α34 = 2,37 ; ε_α56 = 1,64 ; ε_α78 = 2,35 ; ε_α910 = 1,89 ; ε_α1112 = 2,78

ε_α1314 = 9,57

Fig.16

III. Calculul fortelor din angrenajul cilindric cu dinti drepti

Fortele nominale din angrenajul cilindric cu dinti drepti se determina functie de momentul de torsiune motor existent pe arborele pinionului . Forta normala pe dintele pinionului F_n1 , aplicata in mod conventional in punctul de intersectie al liniei de angrenare cu cercul de divizare , se descompune intr-o forta tangentiala F_t1 si una radiala F_r1 la cercul de divizare . Aceste forte au ca reactiuni fortele din roata conjugata (vezi fig.17).

Intrucat pierderile de putere din angrenaj sunt mici (0,5 - 2,5 %) , se neglijeaza influenta lor . In consecinta , fortele din angrenaj care actioneaza asupra celor doua roti sunt egale si de sens contrar . Se considera ca aceste forte actioneaza pe cercurile de divizare ale rotilor .

Fig.17

- Fortele tangentiale

- Fortele radiale F_r1 = F_r2 =F_t1∙tgα

F_r1 = F_r2 = 3935,66 N

F_r3 = F_r4 = 3373,42 N

F_r5 = F_r6 = 2698,73 N

F_r7 = F_r8 = 10574,38 N

F_r9 = F_r10 = 6859,05 N

F_r11 = F_r12 = 5179,28 N

- Fortele normale pe flancul dintelui

F_n1 = F_n2 = 11507,10 N

F_n3 = F_n4 = 9863,23 N

F_n5 = F_n6 = 7890,57 N

F_n7 = F_n8 = 30917,43 N

F_n9 = F_n10 = 20054,54 N

F_n11 = F_n12 = 15143,22 N

IV. Verificarea de rezistenta a danturii angrenajului cilindric cu dinti drepti

A. Verificarea la oboseala prin incovoiere a piciorului dintelui

Tensiunea de incovoiere de la piciorul dintelui se determina cu relatia :

σ_S1,2 - tensiunea de incovoiere la oboseala la piciorul dintelui ;

F_tF1,2 - forta reala tangentiala la cercul de divizare ;

F_tF1,2 = F_t1,2ּK_AּK_VּK_FαּK_Fβ

F_t1,2 - forta nominala tangentiala la cercul de divizare ;

K_A - factorul de utilizare , K_A = 2

K_V - factorul dinamic , K_V = 1,027

K_Fα - factorul repartitiei frontale a sarcinii , K_Fα = 1

K_Fβ = f(K_Hβ) - factorul de repartitie a sarcinii pe latimea danturii ,

K_Fβ = 1,12

b_1,2 - latimea danturii rotilor ;

m - modulul danturii ;

y_F - factorul de forma a dintelui , y_F = 2,625

y_ε - factorul gradului de acoperire y_ε ≥ 0,7

y_ε = 0,25 +0,75 ε_α

σ_FP1,2 - tensiunea admisibila la oboseala prin incovoiere la piciorul dintelui

σ_Flim1,2 - rezistenta limita de rupere prin oboseala la piciorul dintelui

S_FP - factorul de siguranta la rupere prin oboseala la piciorul dintelui ,

S_FP =1,25

Y_N1,2 - factorul nr. de cicluri de functionare , y_N1,2 = 1

Y_S1,2 - factorul concentratorului de tensiune din zona de racordare apiciorului dintelui , y_S1,2 = 1

Y_X - factorul de dimensiune , y_X = 1.

F_tF1,2 = 10813,14ּ2ּ1,027ּ1ּ1,12 = 24875,41 N

b_1,2 = 24,2 mm

y_ε = 0,52 ; σ_FP1,2 = 300/1,25ּ1­ּ1,12ּ1 = 214,28

σ_F1,2 = 24875,41 /49,6ּ2,625ּ0,52 = 205,41 ≤ 214,28

F_tF3,4 = 9268,41ּ2ּ1,027ּ1ּ1,12 = 21321,79 N

b_3,4 = 16,8 mm ; b_3,4 ּm = 16,8ּ4 = 67,2 mm

σ_F3,4 = 21321,79 /67,2ּ2,625ּ0,56 = 213,74 ≤ 214,28

F_tF5,6 = 7414,72ּ2ּ1,027ּ1ּ1,12 = 17057,41 N

b_5,6 = 25,6 mm ; b_5,6ּm = 25,6ּ2 = 51,2 mm

σ_F5,6 = 17057,41 /51,2ּ2,625ּ0,70 = 181,30 ≤ 214,28

F_tF7,8 = 29052,89ּ2ּ1,027ּ1ּ1,12 = 66835,59 N

b_7,8 = 40 mm ; b_7,8ּm = 40ּ2 = 80 mm

σ_F7,8 = 66835,59/80ּ2,625ּ0,56 = 158,02 ≤ 214,28

F_tF9,10 = 18845,11ּ2ּ1,027ּ1ּ1,12 = 43352,79 N

b_9,10 = 56 mm ; b_9,10ּm = 56ּ2 = 112 mm

σ_F9,10 = 43352,79 /112ּ2,625ּ0,64 = 212,40 ≤ 214,28

F_tF11,12 = 14229,98ּ2ּ1,027ּ1ּ1,12 = 32735,78 N

b_11,12 = 16,8 mm ; b_11,12ּm = 16,8ּ2 = 33,6 mm

σ_F11,12 = 32735,78 /33,6 ּ2,625ּ0,51 = 193,32 ≤ 214,28

B. Verificarea solicitarii statice de incovoiere a piciorului dintelui la incarcare maxima

Calculul urmareste evitarea deformatiilor plastice ale dintilor cu duritate mai mica de 350 HB , respectiv ruperea fragila prin soc a danturilor durificate superficial (DF ≥ 350 HB).

Tensiunea maxima de incovoiere la piciorul dintelui este data de relatia :

in care :

K_Amax - factorul de soc maxim ,

M_tmaxp - momentul de torsiune maxim care poate apare la pornire , la oprire sau in cazul blocarii accidentale a transmisiei in timpul functionarii ;

M_tp - momentul de torsiune nominal pe arborele pinionului ;

σ_FPSt - tensiunea admisibila la solicitarea statica prin soc a piciorului dintelui

σ_r - rezistenta de rupere statica prin incovoiere , σ_r = 620 N/mm²

S_FPSt - coeficientul de siguranta la solicitarea statica prin soc a pinionului dintelui Se adopta S_FPSt = 2 .

C. Verificarea la presiune hertziana , in cazul solicitarii la oboseala a flancurilor dintilor (verificarea la pitting)

Tensiunea hertziana de contact de pe flancul dintilor aflati in angrenare se determina in punctul de tangenta al cercurilor de rostogolire (polul angrenarii)

Z_E - factorul modulului de elasticitate al materialului , Z_E = 189,8

Z_H - factorul zonei de contact

Z_ε - factorul gradului de acoperire ,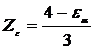

K_Hα - factorul repartitiei frontale a sarcinii , K_Hα = 1,017

K_Hβ - factorul de repartitie a sarcinii pe latimea danturii , K_Hβ = 1,06

b₂ - latimea minima de contact a danturii , b₂ = 48 mm

d₁ - diametrul cercului de divizare , d₁= 120 mm

u - raportul numerelor de dinti (Z₂/Z₁) , u = 0,33

σ_HP1,2 - tensiunea hertziana admisibila la solicitarea de oboseala a flancurilor dintilor ;

S_HP - factorul de siguranta la pitting S_HP = 1,15

σ_Hlim1,2 - rezistenta limita la oboseala superficiala de contact a flancurilor dintilor (la pitting) , σ_Hlim1,2 = 575 N/mm²

Z_R1,2 -factorul rugozitatii flancurilor dintilor , Z_R1,2 = 1

Z_W - factorul raportului duritatii flancurilor , Z_W = 1

Z_L - factorul influentei ungerii , Z_L = 1

Z_V - factorul influentei vitezei periferice a rotilor , Z_V = 1,040

Z_N1,2 - factorul numarului de cicluri de functionare , Z_N1,2

V. Predimensionarea arborilor si alegerea capetelor de arbori

VI. Calculul reactiunilor si trasarea diagramelor de momente

Arborele I

(Miy)_B=0 R_Ay∙195-11507∙67/2-3935∙85=0 R_Ay=3692

(Miy)_A=0 F_a21∙67/2+3935∙110-R_By∙195=0 R_By=4196

(Mix)_B=0 R_Ax∙195-F_t21∙85=0 R_Ax=4713

(Mix)_A=0 F_t21∙110-R_Bx∙195=0 R_Bx=6099

Arborele II

(Miy)_D=0 R_CY∙346+11507∙114/2+3935∙246-9863∙141/2-3373∙52=0

R_Cy= - 2176,79

(Miy)_C=0 655899 + 3935∙100-695341-3373∙294-R_Dy∙346=0

R_Dy= -1842,78

(Mix)_D=0 R_Cx∙346-9268∙246-18845∙52=0 R_Cx=9421

(Mix)_C=0 9268∙100+18845∙294-R_Dx∙346=0 R_Dx=18691

Arborele III

(Miy)_E=0 3373∙267+9863∙110/2-R_Fy∙348=0 R_Fy=4146

(Miy)_F=0 R_Ey∙267-3373∙81-9863∙110/2=0 R_Ey=3054

(Mix)_F=0 R_Ex∙348-18845∙81=0 R_Ex=4386

(Mix)_E=0 18845∙267-R_Fx∙348=0 R_Fx=14458

Bibliografie

1.      Gheghea I..Masini-unelte si agregate .Editura Didactica si Pedagogica Bucuresti ,1983

2.      Ispas C....Masini -unelte .Mecanisme de reglare .Editura Tehnica,

Bucuresti ,1997

3.      Ispas C. ...Masini-unelte .Incercare si receptie .Editura tehnica ,

Bucuresti ,1998

4.      Moraru V. ,Ghionea A. ....Proiectarea masinilor-unelte.Indrumar de proiectare.

5.      Olaru A.....Organologie masini si utilaje . Universitatea Politehica din Bucuresti ,1994

6.      Oprean A. ...Bazele aschierii si generarii suprafetelor . Editura Didactica si PedagogicaBucuresti ,1981

7.      Vlase A.Tehnologia Constructiilor de masini ,Editura Tehnica , Bucuresti ,1997

8.      Ioan Filipoiu....Proiectarea transmisiilor mecanice ,Bucuresti,2001

9.      Stefanuta Enache,.....Proiectarea asistata a sculelor aschietoare

10.   Vasile Moraru ,......Teoria si proiectarea mas.-unelte