Studiul erorilor de prelucrare si de masurare prin metode statistice

STUDIUL ERORILOR DE PRELUCRARE

SI DE MASURARE PRIN METODE STATISTICE

1. Notiuni de teoria probabilitatilor si statica matematica

In fabricatia de serie, ca in diferite alte domenii de activitate, se intalnesc diferite evenimente ca rezultat al experimentelor ce au loc.

Se numeste eveniment E orice rezultat al unui experiment. Astfel, de exemplu, valoarea obtinuta la executarea unei dimensiunii a unui produs constitue un eveniment.

Se deosebesc:

evenimente sigure, care se produc cu certitudine, la orice efectuare a experimentului;

evenimente imposibile, care nu se pot produce la efectuarea unui experiment;

evenimente aleatoare (stahostatice, intamplatoare), care se pot realiza sau nu.

In fabricatie, de exemplu dimensiuile produselor sunt marimi (variabile) intamplatoare, putand lua, intr-un interval dat diferite valori, cu anumite probabilitati (sanse) de realizare.

Se deosebesc: [1-2], [8-9], [11-12], [19-20], [22]

variabile (marimi) aleatoare discrete - care intr-un interval dat pot lua numai anumite valori;

variabile (marimi) aleatoare continue - care intr+un interval dat pot lua absolut orice valori.

Probabilitatea "P" a unui eveniment intamplator "A" este egala cu raportul dintre numarul "m" de cazuri favorabile producerii evenimentului si de numarul total "n" de cazuri (rezultate) probabile :

(1)

Exemplu:

La aruncarea unui zar, probilitatea de a iesi unul din numerele 1 ÷ 6 este P = 1/6.

Pentru m = 0 rezulta: P(E) = 0 (eveniment imposibil);

Pentru m = n rezulta: P(E) = 1 (eveniment sigur).

Prin urmare (2):

0 ≤ P(E) ≤ 1 (2)

Dupa legatura dintre ele, evenimentele intamplatoare pot fi independente, cand realizarea uneia nu influienteaza probabilitatea aparitiei celorlalte, sau dependente, atunci cand realizarea lor se conditioneaza reciproc. Evenimentele pot fi compatibile cand se pot produce simultan si incompatibile cand se exclud reciproc.

Regula adunarii si inmultirii probabilitatilor

Din punct de vedere al complexitatii, evenimentele intamplatoare se clasifica in simple si complexe. Cu evenimentele aleaoare se pot face diferite operatii dintre care mai uzuale sunt reuniunea (adunarea) si intersectia (inmultirea). [1], [8-9], [12], [15], [19], [22]

Reuniunea formeaza un eveniment complex total si consta din realizarea a cel putin unuia din evenimentele considerate. (3):

A B C = A sau b sau C (3)

Probabilitatea aparitiei evenimentului total este egala cu suma probabilitatilor evenimentelor componente (4):

P_t = P(A) + P(B) + P(C) (4)

Exemplu:

Probabilitatea aparitiei la aruncarea cu zarul a numarului 1 sau 4 este: P_t = 1/6 + 1/6 = 2/6 = 1/3.

Intersectia formeaza un eveniment complex compus ce consta din realizarea simultana sau succesiva, a tuturor evenimentelor componente considerate (5):

A B C = A si Bsi C (5)

Probabilitatea aparitiei evenimentului compus este egala cu produsul probabilitatilor evenimentelor componente (6):

P_c = P(A) P(B) P(C) (6)

Exemplu:

Daca se presupune ca in cazul unei asamblari alezaj-arbore, probabilitatea aparitiei alezajelor cu abateri efective cuprinse intre si m este P₁ = 0,4 iar probabilitatea obtinerii arborilor cu abateri efective intre si m este P₂ = 0,35 atunci probabilitatea asamblarii impreuna a acestor alezaje cu acesti arbori va fi:

P_c = P₁ P₂ = 0,4 * 0,35 = 0,14

Din cele doua reguli rezulta ca probabilitatea aparitiei evenimentului total este mai mare decat probabilitatea aparitiei oricaruia din evenimentele componente, iar probabilitatea aparitiei evenimentului compus este mai mica. In practica se intalnesc cazuri cand cele doua reguli se aplica impreuna.

Daca se studiaza o colectvitate de variabile aleatorii (dimensiuni sau abateri relative, valori ale jocurilor sau strangerilor obtinute la asamblare, erori de masurare, etc.) se constata ca acestea, in ansamblu asculta de anumite legi de repartitie (repartitii de probabilitate).

Daca variabila aleatoare ia argumentele x₁, x₂, ., x_n cu probabilitate P(x₁), P(x₂ ),., P(x_n), atunci expresia:

(7)

se numeste repartitie de probabilitate si arata corespondenta dintre argumentele si probabilitatile respective.

Observatie (8):

(8)

Daca in locul unei variabile discrete se considera o variabla continua X, operatorul este inlocuit cu operatorul integrala definita iar relatia precedenta devine (8

    (8΄)

in care:

functia f(x) se numeste densitate de probablitate. [2], [8-9], [11-12], [15], ]17], [19], [20], [22]

Daca intervalul [a,b] devine relatia va fi (9):

(9)

Marimea sau caracteristica continua x" poate fi reprezentata grafic, de exemplu ca in figura.13 1:

Fig. 1. Curba de distributie a unei

marimi intamplatoare continue

Pe axa absciselor se afla diferite valori ale marimi respective, iar pe axa ordonatelor este dat numarul de cate ori se repeta fiecare valoare, respectiv frecventa absoluta a fiecarei calori a lui "x". Probabilitatea ca marimea "x" sa ia valori in intervalul elementar cu baza "dx" si inaltimea "y

In general, probabilitatea ca marimea "x" sa ia valori in intervalul de la x₁ la x₂ este egala cu suprafata limitata de curba si de axa absciselor intre punctele x₁ si x₂ si se exprima prin relatia (10) :

(10)

In consecinta, probabilitatea ca o anumita caracteristica sa ia anumite valori intr-un interval dat se determina pe baza unei legi de distributie care este expresia legaturii dintre valorile caracteristice "x" si probabilitatea corespunzatoare P

2. PRINCIPALII PARAMETRII STATICI CE INTERVIN

IN STUDIUL ERORILOR DE PRELUCRARE SI MASURARE

Marimile aleatoare au o serie de valori carateristice denumite si parametrii statici. Acestia sunt de doua categorii: [1-2], [8-9], [11-12], [18-19], [20], [22]

a - Parametri de tendinta: media aritmetica , media Me, modulul Mo si valoarea centrala x_c

b - Indici de imprastiere: abaterea medie patratica , dispersia D = ∂² si amplitudinea

Valoarea medie aritmetica ( a sirului este data de relatia (11):

(11)

in care:

x₁, x₂, ., x_n - valorile masurate

Deoarece o serie de valori se repeta, vor exista numai "k" valori distincte, daca m₁, m₂, ., m_k reprezinta frecventele valorilor x₁, x₂, ., x_k rezulta ca media aritmetica devine (12.12):

(12)

Cum raportul dintre frecventele absolute si numarul total de valori reprezinta frecvente relativa (probablistica (13))

(13)

Rezulta (14):

Mediana (Me este valoarea absoluta dintr-un sir statiatic ordonatz crescator sau descrescator fata de care frecventa (numarul) valorilor mai mici decat ea este egal cu frecventa (numarul) valorilor mai mari decat ea (15), (16):

- pentru "n" impar (15)

- pentru "n" par (16)

Modulul (Mo reprezinta valoarea observata cu frecventa absoluta sau relativa cea mai mare. (17)

(17)

Valoarea centrala (x_c a sirului static reprezinta semisuma valorilor extreme. (18)

Media aritmetica, mediana, modulul si valoarea centrala sunt parametrii statici ce indica asa numita tendinta de centrare, adica de concentrare a majoritatii valorilor lui "x" intr-o zona de mijloc, prin aceasta determinandu-se pozitia intregii colectivitati sau probe.

Dispersia colectivitatii D(x) = Pentru a se vedea abaterile (dispersia) valorilor x_i fata de valoarea media se considera diferentele (x_i - ), iar intrucat acestea pot fi negative sau pozitive, se iau patratele acestora (x_i - Ca urmare, dispersia colectivitatii va fi :

- pentru marimi continue (19):

(19)

- pentru marimi discontinue (20)

(20)

Abaterea medie patratica (d) considerata unitate de masura a imprastierii, mai este denumita si abatere standard. Ea este egala cu radacina patrata a dispersiei.

- pentru marimi continue (21):

(21)

- pentru marimi discontinue (22)

(22)

Amplitudinea (ω sirului de date este data de diferenta dintre valoarea maxima si minima a sirului static. (23)

(23)

Abaterea relativa medie patratica (λ este data de relatia (24):

(24)

Pentru legea de distributie normala, considerata ca etalon, = 6T, rezulta

Daca se considera amplitudinea egala cu toleranta = T, rezulta = 6d/T

Coeficientul de imprastiere relativa (k este raportul dintre abaterea relativa medie patratica pentru legea de distributie considerata si abaterea relativa medie patratica a distributiei etalon (25):

Coeficientul de asimetrie relativa ( caracterizeaza deplasarea valorii medii fata de mijlocul campului de toleranta (valoarea centrala) x_c

Cum se observa, coeficientul de asimetrie selativa, poate fi pozitiv, negativ sau zero, ceea ce indica existenta sau nexistenta si sensul asimetriei.

Dintre parametri statici prezentati, media aritmetica si abaterea medie patratica, au o semnificatie si importanta deosebita in studiul erorilor de prelucrare si masurare si analiza proceselor tehnologice de executie a pieselor in constructiile de masini.

Observatie:

Pentru marimi intamplatoare independente (27):

3 LEGI DE DISTRIBUTIE

Exceptand influenta unor factori sistematici, o anumita caracteristica cercetata, ia la prelucrarea si masurarea pieselor diferite valori intamplatoare cuprinse intre doua valori limita, fiecare valoare avand o frecventa proprie (un numar de repetari). Caracterul repartizarii acestor valori (cu frecventele lor) intre cele doua valori limita poate fi reprezentat printr-o lege de distributie. In legatura cu marea varietate de caracteristici cercetate in industrie, sau stabilit mai multe legi de distributie mai des utilizate in constructii de masini. [1], [8], [12], [19-22].

3.1. Legea distributiei normale (distributia Gauss sau Gauss-Laplace)

Daca factorii care determina dispersia dimensiunilor efective sunt accidentali, de acelesi ordin, independenti si in numar mare, atunci legea de repartitie a dimensiunii efctive, ca variabila aleatoare, este legea de distributie normala (legea lui Gauss). [!1-2], [8-9], [11-12], [15], [17], [19-22]

Deoarece in productia de serie si de masa, la prelucrarea prin metoda obtinerii automate a dimensiunilor, cele mai multe distributii experimentale sunt foarte apropiate de distributia normala, aceasta este considerata ca repartitie etalon. Expresia analitica a legii lui Gauss, reprezentand functia densitate de probabilitate care depinde, inafara de argumentul "x" si de parametrii si d ) este 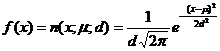(28):

(28)

Curba functiei densitate de probabilitate are forma de clopot, fiind simetrica fata de axa corespunzatoare centrului de grupare a abaterilor. Alegand un sistem de axe, in care axa coordonatelor coincide cu axa de simetrie a curbei f(x), expresia distributiei normale ia forma din fig.2: (29) [1-3], [8-9], [11-12], [15], [17], [19-22]

Fig. 2. Graficul densitatii de probabilitate pentru

legea distributiei normale

(Gauss - Laplace)

(29)

Acest caz corespunde, de, exemplu, masurarii pieselor din seria de fabricatie cu ajutorul aparatelor comparatoare reglate la zero pentru dimensiunea nominala, daca abaterile limita prescrise sunt simetrice fata de aceasta (exemplu:

Curba prezinta doua puncte de inflexiune de abscisa -d si +d, in acest interval, aria suprafetei de sub curba reprezentand 68,27 % din cea totala (ceea ce arata ca aici se gasesc concentrate valorile variabilei aleatoare). Curba tinde asimptotic la axa absciselor si prezinta un maaxim () pentru x

In intervalul de la -3d la +3d suprafata cuprinsa intre curba si axa absciselor constitue 99,73 % din intreaga suprafata, ceea ce face ca intervalele (-∞, -3d) si (+3d, +∞) sa poata fi practic neglijate. [1-2], [9], [11-12], [15], [17], [20], [22]

Ca urmare, intervalul de imprastiere ω = 6d, iar abaterile limita fata de centrul gruparii au valorile ±3d. Conform legii de probabilitate, tinand cont de relatia cunoscuta rezulta (30):

(30)

Integrala unei curbe de repartitie intre anumite valori se numeste functie de repartitie (sau de probabilitate). Functia de repartitie a distributiei normale se noteaza cu N(x, μ, d) si are pe intervalul ( expresia (31):

(31)

In general, probabilitatea ca variabila x sa ia valori in intervalul de la x₁ la x₂ este data de exprersia (32):

(32)

De cele mai multe ori, legea distributiei normale se aplica sub forma normala. In acest sens se face inlocuirea (33):

(33)

Si rezulta (34):

(34)

Intrucat curba normala sub forma normala este simetrica fata de axa ordonatelor, cele doua arii situate de-o parte si de alta a acestei axe sunt egale. (35)

(35)

Ca urmare functia de repartitie normata F(z) va fi (36):

(36)

Functia se numeste functia lui Laplace si este tabelata pentru valorile lui z variind de la la din in . Din motive de simetrie (37):

(37)

Functia de repartitie F(x) este legata de functia lui Laplace prin relatia (38), (fig.3):

Fig. 3. Densitatea de probabilitate in cazul

distributiei normale normate

(38)

Observatii:

1) Probabilitatea ca variabila X sa aiba valori mai mici decat o valoare data a lui x este (39):

(39)

2) Probabilitatea ca variabila X sa aiba valori mai mari decat o valoare data a lui x este (40):

(40)

3) Probabilitatea ca variabila X sa aiba valori cuprinse intre doua valori date x₁ si x₂ este (41):

(41)

4) Daca valorile x₁ si x₂ sunt simetrice fata de media aritmetica respectiv

Un parametru static derivat al legii de repartitie normale il reprezinta abaterea medie patratica relativa definita prin (24):

Acest parametru este util in compararea legii de distributie Gaussiene cu alte legi de distributie.

3.2. Alte legi de distributie ale dimensiunilor

efective

Daca din numarul mare de factori care determina dispersia dimensiunilor unul are o influenta dominanta, atunci se obtin legi de distributie nugaussiene. Repartitia erorilor sistematrice care variaza dupa o lege oarecare poate fi descrisa de diferite functii de distributie. (fig. fig. 7)

De exemplui, erorile cauzate de uzura sculei aschietoare produc o repartitie de egala probabilitate, a carei diagrama are forma unui dreptunghi. (fig. 5)

Fig. 4. Variatie liniara Fig 5. Graficul densitatii de

probabilitate pentru legea distri-

butiei uniforme (egale)

Aceasta lege corespunde cazurilor cand probabilitatea oricarei valori in intervalul dat este, iar in afara lui este nula. [1-2], [8-9], [12], [19-20], [22] Conform legii generale de probabilitate aria dreptunghiului hasurat este egala cu unitatea (43):

(44)

Din cauza unei erori predominante a carei variatie, in prima jumatate a perioadei de timp are un caracter incetinit, iar in a doua jumatate un caracter accelerat, dispersia se face dupa legea lui Simpson reprezentata grafic printr-un triunghi isoscel (fig. 6)

Fig. 6. Graficul densitatii Fig. 7. Variatia

de probabilitate pentru neliniara

distributia dupa legea

triughiului isoscel

Aceasta poate avea originea in limita inferioara a intervalului de imprastiere () sau in centrul gruparii .

3.3. Calculul erorii limita de masurare

Pentru calcularea erorii limita de masurare , erorile componente se grupeaza in erori sistematice, erori intamplatoare si erori grosolane, dupa care se face insumarea acestora. Erorile grosolane nu se iau in considerare intrucat pot fi inlaturate prin sporirea atentiei, inlaturarea defectiunilor, etc. Ca urmare (45):

(45)

In cazul unor metode si mijloace de masurare complexe, eroarea limita totala va fi (46):

(46)

In care:

- erorile limita componente

Orice metoda si mijloc de control este caracterizata de o anumita limita care este data tabelar sau se determina experimental.

4. Studiul erorilor de prelucrare pe cale statica

4.1. Clasificarea erorilor de prelucrare

Dimensiunile si forma pieselor prelucrate nu pot fi obtinute cu o precizie absoluta, prelucrarea fiind insotita de erori. Ca si erorile de masurare, erorile de prelucrare se clasifica in trei mari grupe: erori sistematice, erori intamplatoare, si erori grosolane. [1], [8-9], [11-12], [20]

Erori sistematice Sunt erori ale caror cauze pot fi cunoscute sau determinate si ale caror valori sunt constante sau variabile dupa anumite legi. Ele sunt de mai multe tipuri:

constante cand intervin cu aceeasi valoare (exemplu: erorile la diametrul unui alezaj);

variabile intr-un sens (exemplu: erorile cauzate de uzura sculei);

variabile periodic (exemplu: erorile cauzate de variatia pasului rotilor dintate)

In general, aceste erori pot fi diminuate sau compensate prin reglaje corespunzatoare.

Erori intamplatoare Sunt erori care variaza la intamplare (ca valoare si semn). Ele nu pot fi stabilite in prealabil si nu pot fi inlaturate, dar, cu ajutorul statistici matematice se poate determina influenta lor asupra preciziei de prelucrare. Cauzele lor pot fi: deformatii elastice neuniforme in timp ale sculelor, pieselor, dispozitivelor, variatia proprietatilor fizico-mecanice ale materialului prelucrat, formarea si eliminarea taisului de depunere, etc.

Erori grosolane. Sunt erori care intervin cu valori exagerate, dsenaturand in mod evident rezultatele prelucririi si care apar foarte rar. Se datoresc fie neatentiei operatorului fie defectarii mijloacelor de lucru. Nu se ia an considerare lastudierea rezultatului prelucrarii.

4.2. Studiul erorilor de prelucrare prin metoda

staticii empirice

Ca si erorile aleatoare nu pot fi prevazute sau determinate, ele variind la intamplare atat ca marime cat si ca sens. Influenta lor asupra preciziei de executie se poate determina printr-un studiu statistic al rezultatelor masuratorilor efwectuate asupra unui lot de piese executate pe o masina-unealta, in cadrul aceluiasi reglaj.

Daca pentru executat este important numai ca dimensiunile efective obtinute sa fie cuprinse in limitele prescrise, indiferent de modul in care acestea se distribuie in campul de tolerante, pentru montaj repartitia lor in campul de tolerante poate fi extrem de important. In plus, calcularea anumitor parametrii statici este absolut necesara pentru a se putea face comparatia cu valorile prescrise de proiectant si a se trage concluzii asupra modului in care s-au executat piesele respective, asupra eventualelor rebuturi care au aparut, cauzele acestora si in final, stabilirea de masuri pentru eliminarea lor.

Rezultatele masurarii unui lot (esantion) de piese se pot prelucra statistic prin metoda empirica sau prin calcul.

Metoda staticii empirice consta in sistematizarea rezultatelor masurarii unui numar de 200 ÷ 500 piese executate in aceleasi conditii, prelucrarea si reprezentarea grafica a acestor rezultatesi, in ultimainstanta, compararea lor cu prescriptiile din desenul de executie al piesei sau din standardele corespunzatoare. Pe baza concluziilor trase in urma prelucrarii si interpretarii rezultatelor masurarii celor 200 ÷ 500 piese , se pot lua masurile corespunzatoare impuse so se poate continua prelucrarea. [1], [6], [8-12], [19-20], [22]

Daca, de exemplu, piesele prelucrate sunt arbori la care ne intereseaza obtinerea cu precizie a diametrului, etunci fiecare arbore constitue o unitate statistica, iar caracteristica statica urmarita este diametrul acestora.

Valoarea x_j obtinuta prin masurarea diametrului arborelui se numeste valoare observata. In prima etapa:

- valorile x_j se inscriu in ordinea aparitiei lor.

Sub aceasta forma de inregistrare, valorile obtinute dau o singura informatie: intervalul real de variatie a diametrelor (x_min, x_max). Se impune o a doua etapa:

- ordonarea valorilor dupa rang (in ordinea crescatoare sau descrescatoare), fiecare valoare distincta (diferita) fiind scrisa o singura data, iar in dreptul ei trecandu-se numarul de cate ori se repeta aceasta (frecventa absoluta).

Aceasta ordonare (in sir statiatic) furnizeaza furnizeaza mai multe informatii:

1 - marimea intervalului real de variatie a diametrului,

2 - numarul de piese cu diametre efective in afara tolerantie prescrise (mai mici decat diametrul minim si mai mari decat diametrul maxim)

3 - o imagine aproximativa a distributiei diametrelor efective intre cele doua limite.

Pentru a obtine o imagine mai sugestiva asupra procesului de de prelucrare a usura analiza rezultatelor se trece la a treia etapa:

- se face o grupare statistica care consta din repartizarea valorilor observate intr-un numar de k = 3 ÷ 15 de intervale de grupare egale, numite clase. Pentru fiecare clasa se determina media aritmetica sau valoarea centrala, calculata pe baza limitelor clasei si se calculeaza frecventa absoluta (numarul de piese cu dametrul efectiv cuprins in limitele clasei). Diferenta intre doua limite consecutive de acelasi fel se numeste amplitudinea clasei 'a'

(47)

In care:

x_j x_j-1 - valoarea centrala a doua clase consecutive

Se observa ca dupa grupare toate valorile unei clase sunt tratate ca si cum ar fi egale cu valoarea centrala a acesteia, fapt permis, tntrucar eroarea introdusa este neglijabila. [1], [8-12], [19-20], [22]

Cunoscancu-se frecventa absouta se determina si frecventa relativa in procente,calculata prin impartirea frecventei absolute a fiecarei clase la numarul total de valori si inmultirea rezultatului cu 100 (frecventa relativa de fapt probabilitatea ca diametrul sa ia valori cuprinse intr-o anumita sau anumite clase si sa o imagine sugestiva asupra distributiei diametrelor.

Cu aceste date se intocmeste un tabel centralizator numit tabelul static al frecventelor sau distriubutia de frecvente. Distributia de frecvente, repartitia empirica, poate fi reprezentata grafic sub forma de histograma, poligon de frecvente sau curba empirica de distributie. [1], [6], [8-12], [19-20], [22]

In general, diagramele de frecventa se intocmesc intr-un sistem de coordonate rectanfulare, avand in abscisa valorile dimensiunii observate iar in ordonata frecventa absoluta sau relativa.

Histograma se obtine prin construirea unor dreptunghiuri care au ca baza, pe baza absciselor, amplitudinea claselor in ordinea corespunzatoare, iar ca inaltime, pe axa ordonatelor, frecventa absoluta a fiecarei clase (la o scara convenabila). (fig. 6.)

Fig. 8. histograma de distributie

ω - campul de imprastiere

Td - toleranta la diametrul d

Daca se unesc mijloacele laturilor superioare ale dreptunghiurilor histogramei (corespunzand valorilor centrale ale claselor), se obtine poligonul frecventei. (fig. 9.)

Curba empirica de distributie se obtine trasand o linie curba prin punctele de coordonate (x_j n_j). Pentru ca aceasta curba sa caracterizeze intregul proces de prelucrare si nu numai prelucrarea celor 300 piese se recomanda ca ea sa fie trasata printre puncte, pentru a o apropia de curba de distributie normala (evident daca rezultatele prelucrarii si masurarii pieselor sunt afectate numai de erori intamplatoare). (fig. 10.)

Fig. 9. Poligon de frecvente    Fig. 10. Curba empirica de

distributie

Datele din tabelul fecventelor si graficele se interpreteaza astfel: daca in tabel, frecventele absolute cresc de la valorile, respectiv clasele periferice spre valorile, respectiv clasele din mijlocul intervalului se poate trage concluzia ca rezultatele sunr afectate numai de erori intamplatoare si distributia lor in cele doua limite poate fi asimilata cu cea normala.

Intervalul de variatie a dimensiunilor 'ω' este caracteristica oricarei masini-unelte si de aceea se poate numi toleranta masinii-unelte.

Prin compararea tolerantei masinii ( ) cu cea prescrisa in cazul dat (T_d) se trag concluzii daca masina respectiva este bine aleasa sau nu.

Daca pe axa absciselor diagramelor de frecventa se trec valorile limita prescrise (d_min d_max) portiunea din grafic cuprinsa intre d_min si d_max reprezinta cantitatea absoluta sau procentuala de piese bune iar portiunile ramase, cantitatea de piese rebut.

Metoda statisticii empirice se aplica obligatoriu si la determinarea stabilitatii statice a proceselor tehnologice, in cadrul analizei care precede aplicarea controlului statistic.

Metoda bazata pe calculul statistic (metoda staticii empirice) consta din calcularea unor valori caracteristice ca: media aritmetica si abaterea madie patratica d si compararea acestora cu valorile pre4scrise corespunzatoare (valoarea centrala x_c, toleranta T_x, etc).

4.3. Distributii afectate de erori sistematice

De foarte multe ori, in productia de serie si de masa, dimensiunile pieselor rezultate in urma prelucrarii pe masinile-unelte sunt afectate si de erori sistematice.

Una din cele mai importante cauze ale erorilor sistematice este uzura sculelor aschietoare, care la prelucrarea continua a unui numar mare de piese pe aceeasi masina-unealta, cu acelasi reglaj la diametru, imprima fie o tendinta de marire a dimensiunii (arbori), fie una de micsorare a ascestora (alezaj). [1], [12]

Daca de exemplu, in cazul prelucrarii si pe un strung a unui numar mare de piese, se masoara la intervale egale de timp piesele rezultate, se constata, dupa prelucrarera statistica a datelor (separat pentru loturile masurate la respectivele intervale de timp) ca se obtin curbe de distributie identice dar asezate in pozitii diferite. Declararea lui de la o curba la alta este determinata tocmai de uzura sculei. Daca insa s-ar prelucra static rezultatele obtinute prin masurarea tuturor pieselor prelucrate s-ar trasa o diagrama unica si aceasta ar avea o forma aplatisata datorita existentei erorii sistematice respective. [1], [8-9], [12], [22]

In aceasta situatie, intervalul de imprattiere a valorii diametrului realizat cu acelasi reglaj si fara reascutirea sculei va fi (48), fig.11: [1], [8]

In care:

- campul de imprastiere datorat erorilor intamplatoare

- eroarea sistematica

Fig. 11. Distributia afectata de o eroare sistematica

5. DISTRIBUTIA JOCURILOR SI STRANGERILOR EFECTIVE IN AJUSTAJE

Dupa cum s-a aratat, jocul si strangerea constitue marimi caracteristice ale ajustajelor. Dar atat valoarea jocului cat si a strangerii sunt functie de valorile dimensiunilor efective ale arboriluii alezajului. Ca urmare, distributia valorilor efective ale jocului si strangerii intre cele doua limite (J_min J_max) respectiv (S_min S_max) este determinata de distributia valorilor efective ale dimensiunilor alezajului tntre cele doua limite (D_min D_max) si de distributia valorilor efective ale diametrului arborelui intre cele doua limite (d_min d_max

Considerand, in cazul proceselor tehnologice cu desfasurare normala, ca valorile efective ale dimensiunilor alezajului si arborelui se distribuie intre cele doua limite prescrise, dupa legea repartitiei normale, se poate demonstra ca valorile efective ale jocului sau strangerii la asamblare, se vor distribui tot dupa legea normala.

La determinarea abaterii medii patratice a jocurilor, 'd_j' sau a strangerilor 'd₉' trebuie sa se tina seama de faptulca, in timp ce dsimensiunile alezajului, respectiv arborelui, sunt evenimente intamplatoare independente (alezajele si arborii se prelucreaza separat), jocul sau strangerea care apar la asamblare sunt marimi complexe compuse.

Cum, pentru marimi intamplatoare independente (49):

Rezulta (50):

(50)

In care:

se considera numai la ajustajele cu jocuri,

numai la ajustajele cu strangere, iar

la orice fel de ajustaje, inclusiv cele intermediare.

Inmultind cu 6 si stiind ca (51):

Rezulta (52):

(52)

Dar, intervalul de imprastiere al jocurilor efective la ajustaje cu joc, al strapungerilor efective la ajustajele cu strangere, sau al jocurilor si strangerilor efective la ajustajele intermediare, reprezinta de fapt, toleranta probabila sau practica a jocurilor, a strangerilor sau a jocurilor si strangerilor simultan. Ca urmare, putem scrie (53):

Comparand toleranta practica cu cea algebrica (teoretica) se constata ca prima este mai mica decat a doua (54):

(54)

In consecinta, jocurile si strangerile limita practice vorfi diferite dejocurile sau strapungerile limita algebrice (55):

(55)

Cele aratate si demonstrate analitic sunt prezentate grafic an figurile urmatoare, pentru ajustajele cu joc (fig. 12.) si pentru cele cu strangere (fig. 13).

Fig. 12. Distributia jocurilor la un ajustaj cu joc

Fig. Distributia strangerilor la un ajustaj cu strangere

La ajustajele intermediare, suprafata dintre curba si axa absciselor va cuprinde o portiune pentru jocuri in partea dreapta si una pentru strangeri, considerate ca jocuri negative, in partea stanga. Fiecare portiune de sub curba reprezinta probabilitatea de aparitie a jocurilor, respectiv strangerilor (fig. 14.) [1], [12]

Fig. 14. Distributia jocurilor si strangerilor

la un ajustaj intermediar

Din cele prezentate se poate trage o concluzie foarte importanta: prin asamblarea arborilor si alezajelor executati cu o anumita precizie (toleranta) se obtine un ajustaj cu o precizie practica mai mare decat precizia calculata teoretic. Aceasta intrucat valorile jocurilor apropiate de jocurile limita teoretice, ca si ale strangerilor apropiate de strangerile limita teoretice, au o probabilitate practic egala cu zero, ceea ce duce la micsorarea tolerantei ajustajului si la considerarea altor valori limita ale jocurilor si strangerilor mai apropiate una de alta decat valorile limita teoretice. [1]

6. METODE DE CONTROL STATISTIC

Metodele de control statistic bazate pe statistica matematica fac parte din categoria celor mai inaintate metode aplicate in productia de serie ti de masa.

Controlul statistic are urmatoarele functii importante: [1]

a)      - o functie cu carecter pasiv, prin care se depisteaza produsele necorespunzatoare calitativ;

b)      - o functie cu caracter activ si preventiv, care se exercita prin informatiile obtinute si prin indicatiile asupra felului in care trebuie condus procesul tehnologic pentru ca acesta sa fie stabil in timp.

Indiferent de metoda de control static aplicata, analiza premergatoare a procesului de prelucrare este obligatorie, aceasta prevazand verificarea stabilitatii procesului tehnologic din punct de vedere static si dinamic. [1], [8], [11-12], [20], [22]

Pentru verificarea stabilitatii statice se masoara valoarea caracteristicii urmate de primele piese realizate pe o anumita masina-unealta si cu un anumit reglaj. Se prelucreaza datele obtinute prin metoda statici empirice. Daca forma diagramelor de frecventa justifica ipoteza prelucrarii dupa legea repartitiei normale, se considera ca procesul tehnologic este static stabil, si din acest punct de vedere este permisa aplicarea controlului static. Daca nu, procesul tehnologic se supune verificarii pentru e se descoperii cauzele care dau abateri de la distributia normala. Dupa stabilirea si inlaturarea acestor cauze, verificarea stabilitatii statice se reia de la inceput. [1], [11-12], [20], [22]

Pentru verificarea stabilitatii dinamice se pregatasc doua formulare: unul sub forma de tabel si unul sub forma de diagrama. In timpul prelucrarii se extrag la intamplare probe de cate cinci piese, de exemplu, luate la intervale nu mai mici de 30 minute, dintre piesele prelucrate in perioada imediat anterioara. Acestea se masoara cu un aparat de precizie corespunzatoare, valorile obtinute trecandu-se in formularul tabel, in coloana corespunzatoare datei si orei la care s-a efectuat extragerea. (fig. 15.)

Se calculeaza apoi media aritmetica si amplitudinea _i corespunzatoare celor tcinci valori pentru fiecare proba. Dupa cel putin 25 de probe se calculeaza mediamediilor aritmetice si amplitudinea medie a tuturor probelor luate. (56)

(56)

In care:

k - numarul probelor.

Fig. 15. Formular tabel pentru verificarea stabilitatii

dnamice a procesului tehnologic

Fig. 16. Formular diagrama pentru verificarea stabilitatii

dinamice a procesului tehnologic

Formularul diagrama se imparte in doua parti. (fig. 16). in partea superioara - spatiul mediilor - se traseaza o linie in dreptul valorii , precum si doua linii (L_cs L_ci) semnificand limitele de control superioara si inferioara a mediei. In partea inferioara - spatiul amplitudinilor - se traseaza o linie in dreptul valorii L_cs ce semnifica limita de control superioara a amplitudinii. Valorile L_cs L_ci si L_cs' se dau in STAS in functie de valoarea si numarul 'n' al exemplarelor dintr-o proba

Daca mediile tuturor probelor se gasesc intre limitele L_cs si L_ci se considera ca procesul tehnologic este stabilit ca reglaj.

Daca amplitudinea tuturor probelor au valori sub limita superioara de control a amplitudinii L_cs, se considera ca procesul tehnologic este stabil ca precizie.

Daca procesul este stabil si ca reglaj si ca precizie atunci el este dinamic stabil.

Dupa determinarea stabilitatii statice si dinamice a procesului tehnologic se va face o comparatie a starii acestuia cu conditiile prescrise, respectiv se va compara pozitia si marimea campului de imprastiere, cu campul de tolerante prescris. [1], [9], [11-12], [20], [22]

In industria constructoare de masini, se aplica controlul statistic pe baza de masurare, pe baza de mijloace de verificare limitative sau pe baza de verificare la 'corespunzator' sau 'necorespunzator', alegerea metodei adecvate facandu-se din considerente tehnico-economice.

Controlul statistic pe baza de masurare se aplica prin una din urmatoarele variante:

cu fisa de control pentru medie si amplitudine;

cu fisa de control pentru mediana si amplitudine;

cu fisa de control pentru medie si abatere medie patratica.

In general, se examineaza probe care au un numar cuprins intre 2 si 11 exemplare, dar se recomanda ca acestea sa aiba 5 exempare. Se pot utiliza, dupa caz, mijloace de masurare universale sau speciale, la care valoarea diviunii sa fie de minim 1/20 si maxim 1/6 din valoarea tolerantei prescrise.

Prin efectuarea controlul se urmaresc 2 parametri statistici: un parametru care determina pozitia campului de imprastiere, respectiv care da indicasii asupra reglajului masinii-unelte si un parametru care determina marimea campului de imprastiere, respectiv care di indicatii asupra preciziei masinii.