Metoda elementelor finite

METODA ELEMENTELOR FINITE

1.1     Definirea metodei

Metoda elementelor finite (MEF) este o tehnica numerica de analiza a mediilor continue, dezvoltata, cu precadere, pentru cele cu doua si trei dimensiuni (2D si 3D), cu aplicatii preponderent ingineresti (pentru studiul fenomenelor de deformabilitate, transfer de caldura, curgerea fluidelor etc.).

Particularizand-o pentru cazul structurilor, MEF porneste de la idea ca pentru o structura continua, reala (cu geometrie oarecare si conditii la limita complexe), o solutionare exacta nu poate fi efectuata sau daca poate fi efortul de calcul este nejustificat. In cazul in care se posibila o solutionare aproximativa, mai usor de efectuat, si gradul de aproximare este rezonabil inginereste, aceasta devine solutie pentru structura initiala. Altfel spus, analiza cu MEF a unei structuri consta in inlocuirea acesteia cu alta pentru care solutia este mai usor de gasit, rezultatele acesteia fiind aproximative pentru structura initiala, dar acceptabile din punctul de vedere ingineresc.

Inlocuirea structurii de analizat urmeaza unui proces (numit modelare) de impartire (sau discretizare) in subdomenii (numite elemente finite), conectate la extremitatile lor (numite si noduri exterioare ale elementului finit), in nodurile modelului discret cu elemente finite.

Pentru cazul structurilor, MEF poate fi privita ca extinderea metodei staticii matriceale clasice, dezvoltata pentru studiul structurilor din bare (care pot fi tratate si ca elemente finite unidimensionale, 1D) la structuri continue cu elemente finite bidimensionale, 2D si tridimensionale, 3D.

MEF implica un proces de discretizare (naturala sau artificiala) a structurilor analizate, precum si un mod specific de stabilire, pentru fiecare element finit, a ecuatiei matriceale de echilibru (sistem de ecuatii), componentele matricelor si vectorilor ce intervin fiind date, cel mai adesea, sub forma de integrala simpla pentru elementele finite cu o dimensiune, dubla pentru elementele finite cu doua dimensiuni si tripla pentru elementele finite cu trei dimensiuni. Rezolvarea integralelor poate fi exacta, dar cel mai adesea aceasta este aproximativa, apelad la integrari numerice (dupa o directie in cazul elementelor finite 1D, dupa doua directii in cazul elementelor finite 2D si dupa trei directii in cazul elementelor finite 3D).

Principial, analiza unei structuri cu MEF urmeaza aceleasi etape de calcul cunoscute din metoda staticii matriceale clasice.

1.2     Modelarea structurilor cu elemente finite

Discretizarea structurilor nefiind naturala, depinde, calitativ si cantitativ, de experienta si abilitatea analistului de a o efectua.

Urmatoarele observatii trebuie avute in vedere la alcatuirea modelului discret cu elemente finite:

- precizia solutiei in MEF depinde de numarul elementelor finite utilizate la obtinerea modelului discret; solutia aproximativa este mai apropiata de cea exacta cu cat numarul de elemente finite utilizat la discretizare este mai mare (cel putin in principiu), dar si timpul de calcul necesar atingerii acesteia, deci si costul, este mai mare;

- discretizarea trebuie sa surprinda particularitatile de forma, material, rezemare si incarcare pe care structura le prezinta;

- analiza unei structuri se face in mai multe variante de discretizare.

Referitor la particularitatile de forma dar si de comportare a structurii, este de retinut faptul ca elementele finite care pot alcatui modelul discret trebuie sa fie compatibile cu dezvoltarea spatiala a structurii, iar modelul matematic care defineste elementul finit sa simuleze cat mai bine comportarea structurii in zona pe care o acopera. Astfel, in cazul in care structura are o dezvoltare unidirectionala elementele finite corespunzatoare sa fie unidimensionale (1D), drepte sau curbe, la o dezvoltare bidirectionala elementele finite corespunzatoare sa fie bidimensionale (2D), cu laturi drepte sau curbe si la o dezvoltata spatiala elementele finite corespunzatoare sa fie tridimensionale (3D), cu fete plane sau curbe (figura 1.1).

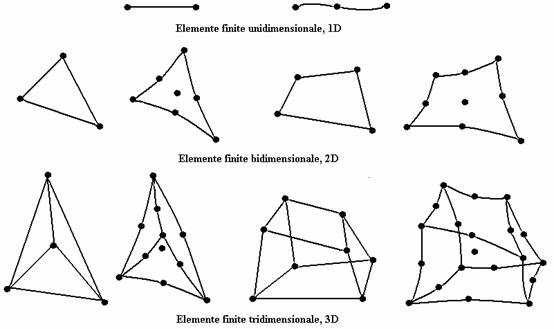
Figura 1.1 Tipuri generice de elemente finite

In afara de extremitati, elementele finite pot prezenta noduri si intre acestea (vezi cazul celor cu laturi curbe) sau la interiorul elementelor finite si care nu se cupleaza in nici un fel altui element finit, numite si noduri necompatibile.

La alcatuirea modelului discret cu elemente finite al unei structuri de analizat se recomanda:

- pozitia nodurilor, respectiv a frontierei elementului finit, sa tina cont de eventuala variatie accentuata a geometriei structurii, de posibilitatea existentei mai multor materiale in alcatuirea structurii, de existenta unor incarcari concentrate sau distribuite discontinuu;

- utilizarea unei discretizari graduale pentru analiza unor zone in care se presupune o variatie pronuntata pentru functia parametru: cazul existentei unor goluri si/sau incluziuni de material, unor sarcini concentrate, unor variatii bruste de geometrie;

- ca in cazul discretizarii structurilor cu frontiera curba sa se utilizaeze elemente finite care sa urmareasca in mod fidel conturul acesteia: fie un numar mare de elemente cu margini drepte, fie un numar mic de elemente cu margini curbe;

- ca raportul lungimilor oricaror doua laturi ale aceluiasi element finit sa tinda la 1, in caz contrar, sa nu depaseasca raportul 1/5.

Finalul metodei elementului finit consta in rezolvarea unui sistem de ecuatii algebrice (ecuatia de echilibru matriceal a modelului discret cu elemente finite) pentru a carui memorare este necesar un efort din partea calculatorului, efort ce depinde nu numai de numarul parametrilor modelului discret, ci si de modul de numerotare a nodurilor acestuia (mai precis a gradelor de libertate asociate elementelor finite).

Marimea spatiului alocat in memoria calculatorului pentru stocarea elementelor matricei sistemului de ecuatii (numita, la modul general, matrice caracteristica a structurii), mai intai la nivelul elementului finit si, ca o consecinta, la nivelul modelului discret, este data de asa numita latime de banda, care trebuie sa fie cat mai mica.

Latimea de banda este data de numarul maxim de coloane care contin macar o componenta diferita de zero, situate la stanga si la dreapta diagonalei principale a matricei caracteristice (componentele din afara latimii de banda fiind egale cu zero). Astfel, pentru fiecare element finit se va urmari realizarea unei diferente minime intre oricare doi indecsi nodali corespunzand extremitatilor sale (mai corect spus intre oricare doua grade de libertate ale elementului finit).

Matricea caracteristica capata semnificatii fizice (de rigiditate sau permeabilitate si flexibilitate sau rezistenta) functie de fenomenul studiat (deformabilitate sau transfer de caldura si curgerea fluidelor etc.) si metoda de rezolvare, respectiv de parametrii principali ai problemei (necunosculele problemei).

In deformabilitate, daca rezolvarea problemei se face prin metoda deplasarilor, parametrii principali (necunoscutele problemei) sunt deplasarile nodurilor modelului discret si matricea caracteristica este de rigiditate elementala sau structurala, dar daca rezolvarea problemei se face prin metoda fortelor, parametrii principali (necunoscutele problemei) sunt fortele din nodurile modelului structural si matricea caracteristica este de flexibilitate elementala sau structurala).

Din considerente de implementare pe calculator a programelor bazate pe MEF, unele forme de exprimare ele acesteia au fost preferate altora. Astfel, in deformabilitate, programele bazate pe MEF, exprimarea in deplasari, cunosc o dezvoltare  ampla, pentru ca sistemul static de baza, de la care incepe procedura de calcul, este unic si deci nu pune probleme de dubiu calculatorului sau evita efortul analistului de depasire a dubiului si riscului strecurarii de erori.