Statica structurilor cu zabrele

STATICA STRUCTURILOR CU ZABRELE

1         Elemente si ansambluri structurale

Zabrea (sau bara dublu articulata) este elementul structural cu o dimensiune geometrica mult mai mare decat celelalte doua, lungimea L, cu aria sectiunii transversale, constanta A, constituit dintr-un material caracterizat de modulul de elasticitate, constant E, la care deplasarile extremitatilor se produc longitudinal sub actiunea fortelor corespunzatoare ce actioneaza pe aceeasi directie (figura 1

Studiul deformarii elementului structural incepe cu identificarea parametrilor proprii, d₁, d₂, f₁, f_2,, raportati la reperul propriu, definit de axa x dispusa longitudinal elementului (figura 1

Figura 1 Element structural tip zabrea in sistemul de axe propriu x

Ecuatia de echilibru static a elementului structural de tip zabrea, stabilita prin metodele staticii structurilor, este data de relatia 1.1a,

                             

sau in exprimare matriceala, compacta, de forma:    (1.1a)

unde: este matricea de rigiditate a zabrelei raportata la parametrii proprii d₁, d₂, f₁, f₂;

 - vectorul deplasarilor extremitatilor zabrelei sau al parametrior proprii principali d₁, d₂;

 - vectorul fortelor ce actioneaza la extremitatile zabrelei sau al parametrilor proprii secundari f₁, f₂.

Structurile cu zabrele se pot organiza dupa o directie (putin interesante), dar de cele mai multe ori dupa doua directii (in plan, figura 2) si dupa trei directii (in spatiu).

Figrura 2 Structura plana cu zabrele in sistemul de axe structural XY

Pentru fiecare nod i al unei structuri cu zabrele plane se definesc cate doi parametri principali, D_2i-1 si D_2i, primul fiind definit ca deplasare dupa prima axa a reperului structurii (obisniut X) si al doilea ca deplasare dupa cea de a doua axa a reperului structurii (obisnuit Y); pentru o structura cu n noduri se definesc 2n parametri principali. Parametrii secundari corespunzatori sunt fortele nodale F_2i-1 si F_2i; pentru o structura cu n noduri se definesc 2n parametri secundari. Parametrii sunt pozitivi daca vectorii ce ii definesc au acelasi sens cu sensul pozitiv al axelor cu care sunt paraleli. Din aceste considerente se poate aprecia ca ecuatia matriceala de echilibru mecanic a structurii plane va fi constituita din 2n ecuatii.

Din necesitatea asigurarii compatibilitatii deplasarilor extremitatilor elementului structural cu deplasarile nodurilor de conectare ale structurii plane, elementul de tip zabrea capata deplasari fictive la extremitati, pe directia transversala axei longitudinale, y, (figura 3), ecuatia de echilibru static, raportata la parametrii proprii fiind data de relatia 1.1b.

Figura 3 Element structural tip zabrea in sistemul propriu x,y

                            (1.1b)

Pentru fiecare nod i al unei structuri cu zabrele spatiale se definesc cate trei parametri principali D_3i-2, D_3i-1 si D_3i, primul fiind definit ca deplasare dupa prima axa a reperului structurii (obisniut X), al doilea ca deplasare dupa cea de a doua axa a reperului structurii (obisnuit Y) si al treilea ca deplasare dupa cea de a treia axa a reperului structurii (obisnuit Z); pentru o structura cu n noduri se definesc 3n parametri principali. Parametrii secundari corespunzatori sunt fortele nodale F_3i-2, F_3i-1 si F_3i; pentru o structura cu n noduri se definesc 3n parametri secundari. Din aceste considerente se poate aprecia ca ecuatia de echilibru mecanic a structurii spatiale va fi constituita din 3n ecuatii.

Din necesitatea asigurarii compatibilitatii deplasarilor extremitatilor elementului structural cu deplasarile nodurilor de conectare ale structurii spatiale, elementul de tip zabrea capata deplasari fictive la extremitati si pe cea de a doua axa transversala axei longitudinale, z, ecuatia de echilibru static, raportata la parametrii proprii fiind data de relatia 1.1c.

               (1.1c)

2         Statica matriceala clasica pentru analiza structurilor plane cu zabrele

2.1     Stabilirea ecuatiei matriceale de echilibru static a zabrelei

Stabilirea ecuatiei matriceale de echilibru static, pentru elementul structural curent e al unei structuri plane cu zabrele, implica parcurgerea unui proces etapizat.

Etapa 1.1. Stabilirea ecuatiei maticeale de echilibru static prin raportare la parametrii proprii, cu proiectarea acestora in sistemul de referinta propriu xy (in aceasta etapa notatiile utilizeaza minuscule si indicele p pentru sistemul de referinta propriu), relatia E1.1,

sau                                                        (E1.1)

Etapa 1.2. Stabilirea ecuatiei matriceale de echilibru static prin raportare la parametrii structurali aferenti, cu proiectarea acestora in sistemul de referinta unic XY (in aceasta etapa notatiile utilizeaza majuscule si indicele S pentru sistemul de referinta structural , relatia E1.2,

sau                                                        (E1.2)

unde, indicele inferior e arata apartenenta parametrului la elementul curent iar indicele superior e cota de participare a elementului curent.

Parametrii proprii ai extremitatilor zabrelei sunt proiectati pe directiile parametrilor structurali aferenti ai nodurilor de conectare, cu ajutorul matricei de transformare prin rotire, T, care are ca elemente componente cosinusii directori ai axelor proprii (x si y) definiti functie de reperul structurii (XY). In acest caz matricea de transformare prin rotire este de forma:

unde: α este unghiul masurat, in sens pozitiv, de la axa de referinta X catre axa de referinta x (antiorar).

Matricea T este o matrice ortogonala si are proprietatea ca inversa coincide cu transpusa:

Relatiile de legatura dintre parametrii proprii si parametrii structurali aferenti  sunt:

                      

care, inlocuite in relatia E1.1 si operat corespnzator, conduc la stabilirea matricei de rigiditate a zabrelei raportata la parametrii structurali aferenti:

In cazul structurilor spatiale cu zabrele, matricea de transformare prin rotire este de forma:

unde: c_x, c_y, c_z sunt cosinusi directori;

.

Etapa 1. Stabilirea ecuatiei matriceale de echilibru static prin raportare la parametrii structurii, obtinuta prin completarea cu ecuatii fictive corespunzatoare parametrilor structurii ce nu sunt aferenti sau nu apartin zabrelei (in aceasta etapa notatiile utilizeaza majuscule sau indici referitori la apartenenta la elementul curent):

sau                                                        (E1.3)

unde:[K]_S este matricea de rigiditatea a elementului tip zabrea raportata la parametrii   structurali.

2.2     Analiza statica a grinzii plane cu zabrele

Enuntarea problemei: Sa se efectueze analiza statica a structurii plane cu zabrele (determinarea deplasarilor nodurilor, fortelor din reazeme si eforturilor din elementele structurale-zabrele), schema statica, caracteristicile geometrice si mecanice, precum si incarcarile fiind precizate pe figura 4.

Rezolvarea problemei

Aplicatia utilizeaza notatii pentru variabile si operatori corespunzand programului de calcul matematic Mathcad (simbolul := are intelesul de atribuire).

Figura 4 Structura cu zabrele si modelul discret corespunzator

Etapa 1, stabilirea ecuatiei maticeale de echilibru static pentru fiecare zabrea:

Zabrea 1 (figura 5.1)

Figura 5.1 Parametri si sisteme de referinta pentru zabreaua 1

Etapa 1.1 - prin raportare la parametrii proprii

                  

Etapa 1.2 - prin raportare la parametrii structurali aferenti

Etapa 1.3 - prin raportare la parametrii structurali

Zabrea 2 (figura 5.2)

Figura 5.2 Parametri si sisteme de referinta pentru zabreaua 2

Etapa 1.1 - prin raportare la parametrii proprii

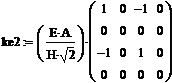
Etapa 1.2 - prin raportare la parametrii structurali aferenti

Etapa 1.3 - prin raportare la parametrii structurali

Zabrea 3 (figura 5.3)

Figura 5.3 Parametri si sisteme de referinta pentru zabreaua 3

Etapa 1.1 - prin raportare la parametrii proprii

Etapa 1.2 - prin raportare la parametrii structurali aferenti

                               

Etapa 1.3 - prin raportare la parametrii structurali

Etapa 2 stabilirea ecuatiei matriceale de echilibru static a structurii

Etapa 3 introducerea conditiilor la limita (cl):

Etapa 4, determinarea deplasarilor necunoscute (nec):

- generarea vectorului deplasarilor:

Etapa 5 (auxiliara), determinarea fortelor din reazeme:

- generarea vectorului fortelor:

Etapa 6 (auxiliara), determinarea eforturilor din zabrele:

Zabrea 1

Zabrea 2

Zabrea 3

3         Stabilirea prin MEF - formularea directa

a ecuatiei matriceale de echilibru static a zabrelei

cu raportare la parametrii proprii

In MEF, stabilirea ecuatiei matriceale de echilibrului static raportata la parametrii proprii, pentru elementul tip zabrea, implica un proces de calcul etapizat.

Etapa 1.1.1. Identificarea problemei.

Fie elementul tip zabrea de lungime L, caracterizat de aria sectiunii transversale, constanta A, si modulul de elasticitate, constant E, cu axa proprie x orientata pozitiv de la extremitatea 1 catre extremitatea 2, deplasarile si fortele actionand la extremitatile sale (figura 6).

Figura 6 Definirea zabrealei ca element finit

Problema consta in gasirea, in sistemul propriu de referinta, a unei relatii intre vectorul parametrilor proprii principali, constituit cu deplasarile extremitatilor zabrelei d₁, d₂, si vectorul parametrilor proprii secundari, constituit cu fortele corespunzatoare f₁, f₂, de forma data de relatia E1.1.1.

                       (E1.1.1)

Etapa 1.1.2. Gasirea functiei, convenabile, de aproximare a deplasarilor d(x).

Se face ipoteza ca pe toata lungimea zabrelei deplasarea d(x) este data de o functie cu variatie liniara (polinomiala), care, matriceal, este de forma data de relatia E1.1.2

sau compact, de forma:                  (E1.1.2)

unde:   este matricea functiei de aproximare;

 sunt coordonatele generalizate ale deplasarii.

Etapa 1.1. Stabilirea relatiei matriceale dintre deplasarea punctuala d(x) si deplasarile extremitatilor zabrelei d₁, d₂.

Se face afirmatia ca relatia E1.1.2 este valabila inclusiv in extremitatile zabrelei si aceasta se poate scrie simultan sub forma matriceala:

de unde rezulta:

care prin inlocuire in relatia E1.1.2 conduce la relatia E1.1.3

sau in forma compacta:                  (E1.1.3)

unde:   N₁(x), N₂(x) sunt functiile de forma ale zabrelei (aferente parametrilor principali), egale cu:

                               

sau, pentru cazul in care originea sistemului de referinta propriu se alege in prima extremitate (x₁=0, x₂=L), egale cu:

      

Functiile de forma sunt functii de pondere, avand proprietatea de a lua valoare maxima (unitara) in extremitatea in care actioneaza parametrul principal aferent, restul functiilor de forma, aferente celorlalati parametri principali, avand valoare minima (zero); suma tuturor functiilor de forma are valoare unitara.

In implementarea pe calculator a programelor bazate pe metoda elementului finit este importanta exprimarea functiei deplasarilor prin intermediul functiilor de forma.

Etapa 1.1.4. Stabilirea relatiei matriceale dintre deformatia specifica punctuala  si deplasarile extremitatilor zabrelei d₁, d₂.

Se pleaca de la definitia deformatiei specifice din rezistenta materialelor aplicata zabrelei, relatia E1.1.4:

sau in forma compacta                   (E1.1.4)

unde:

Etapa 1.1.5. Stabilirea relatiei matriceale dintre tensiunea punctuala  si deplasarile extremitatilor zabrelei d₁, d₂.

Se pleaca de la definirea deformarii elastice din rezistenta materialelor (legea lui Hook) aplicata zabrelei, relatia E1.1.5:

sau in forma compacta                   (E1.1.5)

unde [D] este matricea caracteristicilor mecanice ale materialului;

[H] - notatia consacrata a produsului [D][B].

Etapa 1.1.6. Stabilirea relatiei matriceale dintre deplasarile extremitatilor zabrelei d₁, d₂ si fortele corespunzatoare f₁, f₂.

Se pleaca de la definitia lucrului mecanic, exprimarea in deplasari virtuale (aplicat intregului volum al zabrelei), pentru cel interior:

respectiv exterior:

si se impune egalitatea lor, pentru existenta echilibrului static (L_int L_ext

Dupa egalarea celor doi termeni si efectuarea simplificarilor (considerand ca nu toate deplasarile virtuale sunt egale cu zero) se obtine relatia E1.1.6

sau in forma compacta                   (E1.1.6)

ceea ce coincide cu relatia E1.1.1 si care trebuia gasita.

Integrala ce defineste matricea de rigiditate poate fi rezolvata fie aproximativ, prin integrare numerica dupa o directie, fie exact (si in aceasta situatie este posibil), prin inlocuirea termenilor si efectuarea operatiilor indicate, in final obtinandu-se:

Ecuatia de echilibru static de mai sus este identica cu cea cunoscuta din statica matriceala clasica (1.1a). In felul acesta elementul structural tip zabrea devine element finit tip zabrea, din categoria elementelor finite unidimensionale (1D).