Gaze ideale

GAZE IDEALE

1 Proprietatile gazelor ideale(perfecte). Tipuri de gaze ideale

Gazul ideal este o ideolizare a gazelor reale de care acestea se apropie cu cat presiunea scade spre 0 si temeperatura e mai mare. In natura nu exista gaz perfect aceasta fiind o notiune abstracta care are drept scop sa simplinstalatii frigorificeice teoria si formele de calcul. Teoria cinetico-moleculare permite sa se stab. Pe cale teoretica legile simple ale gazului ideal care are urmatoarele proprietati:

-moleculele gazului ideal sunt perfect sferice si elastice

-gazul ideal contine un nr. foarte mare de molecule considerate punctinstalatii frigorificeorme aflate intr-o miscare permanenta dezordonata inertiala coresp. legilor mecanice clasice

-volumul propriu al moleculelor este neglijabil in raport cu volumul total ocupat de gaz

-fortele de intereactiune moelculara sunt nule (atractia dintre molecule este nula deci energia potentiala conteza numai energia cinetica Ucin≠0)

-presiunea exercitata de gazul ideal depinde de energia cinetica al moleculelor

-gazul intern nu are vazcozitate(frecare interna intre straturile de fluid) nu se lichefieaza fiind mult rarefiat

-caldurile specinstalatii frigorificeice ale gazului ideal sunt constante si sunt independente de temepratura si presiune(Cp=Qspecit=ct; Cv=Qspecit ; V=ct)

In functie de nr atomilor din molecula de gaz ideal aceasta poate fi monoatomic, biatomic, triatomic sau poliatomic rezultand valori dinstalatii frigorificeerite pentru caldurile speciale ale fiecarui tip de gaz ideal.

In instalatia frigorinstalatii frigorificeica agentul termic in stare gazoaza se considera a fi gazul ideal mai ales pe partea de joasa presiune. De aceea se foloseste legile gazului ideal.

Capitolul  2 Legile simple ale gazului ideal. Ecuatia de stare

Legea Boyle Mariotte. La temeperatura constanta pentru o masa const de gaz produsa dintre presiune si volum are o val. const pV – const, T-const sau p1V1 = p2V2

Legea Gay-Lussac. La presiune constanta rap. dintre vol. unei mase const. de gaz si temepratura sa absoluta este constanta.

V/T = const; Pconst sau V1/T1 = V2/T2

Legea Charls. Daca vol. unei mase constante de gaz ideal ramane constant rap. dintre presiune si temp. sa absoluta este constanta.

P/T = ct ; V- const sau p1/T1 = p2/T2

Ecuatia Clapeyron(Ecuatia termica de stare a gazului ideal)

p1V1/T1 = p2V2/T2 = ct

Exprima leg intre marimile de stare pV si T

Pt. m=KgpV/T = ct = R sau pV = RT(1)

R- const care depinde de natura gazului

Daca se multiplica ecuatia 1 cu masa molara M se obtine pVM=MRT- volumul molar

RM- ct universala a gazului ideal care nu depinde de natura lor

Pt. un K mol de gaz ecuatia termica de stare devine:

pVM=RMT

RM=pNVMN/TN = 101 325 N/m patrat ∙ 22, 414/273, 15K=8315J/K mol K

Legea lui Avogadro(K mol)

Volumul egal din orice gaz perfect aflata la aceeasi temp. si presiune contin aceleasi nr de molecule. De aici sa stabilit molul ca unitatate de masura pentru masa adica 1 mol contine 1 nr de grame de gaz ideal egal cu masa sa molara M.

1 mol =M(m) O2 = 321 mol = 32 g sau K mol = 32 kg ; 1 K mol H2 = 2 Kg

In conditii egale de presiune si temp 1 K mol de gaz ideal contine acelasi nr de molecule denumit nr lui Avogadro: NA = 6, 023∙10 la 23 mol/K mol.

Si o cupa la presiune si temp. normale volumul : VM= 22, 414 m cubi

Legea lui Avogradro si val. Volumului molar ( VMN ) sunt riguros valabile numai pentru gazul ideal.

Capitolul  3 Transformarile simple ale gazului ideal. Reprezentarea mecanica a proceselor in diagrama Pv

Relatia lui Robert Mayer care exprima legatura intre caldura specinstalatii frigorificeica la presiune constanta si volum constanta este Cp-Cv = R[J/kg K]

Prin inmultire cu masa molara => MCp – MCv=MR

CMp – CMv = RM unde CMp- caldura specinstalatii frigorificeica molara la p constant

CMv – caldura specinstalatii frigorificeica molara la v constant

Notam K= Cp/Cv = CMp/CMv => Cv= R/k – 1 ; Cp = kRR/k-1

CMv=RM/k-1 ; CMp=kR/K-1

Pentru gaz monoatomic : CMv=3UM/2

CMp=5RM/2

k=CMp/CMr=5/3=1, 66-exponent adiabatic

Pentru gaz viatomic CMv = 5RM/2

CMp=7RM/2

K=CMp/CMv = 7/5=1, 4

Pentru gaz cu mai mult de 2 atomi in molecula:

CMv=6RM/2

CMp=8RM/2

(γ)k=CMp/CMv=8/6=1, 33

Se folosesc la anumite transformari

Reprezentari de procese in diagrama PV:

a)     Transformare izocora => V= constant

P/T constant

Dp>0=>DT >0 P2/T2 = P1/T1 = P2-P1/T2-T1=DP/DT

Q1, 2 >0 ; Q1, 2 – primita

Dp<0=>DT<0=>Q1, 2<0 Q1, 2 – cedata

2. Transformare Izobara

P=cT pV/t=ct=>V/T=ct

L1, 2= mRDT = pDV

DU=mCvDT

Q1, 2 = L1, 2 + DU1, 2=m CvDT+mRDT = m(Cv+R)=mcMDT

Q1, 2 = H2 – H1 = DH1, 2

DH-entalpie

V1/T1=V2/T2 = V2-V1/T2-T1 = DU/DT

Daca DV >0=> DT>0;L1, 2>0;DU>0;Q1, 2>0

Daca DV<0=> DT<0 => L1, 2<0;DU<0 Q1, 2<0

3. Transformare izotermica

pV/T = constant =>pV = ct

L1, 2=p1V1 lnV2/V1 = p1V1 ln p1/p2 = mRT lnV2/V1 = m RT ln p1/p2[J]

DU1, 2=0 deoarece mCv DT=0

Q1, 2=L1, 2 + DU1, 2 => Q1, 2 =R1, 2

L1, 2 –arie suprafetei de sub curba

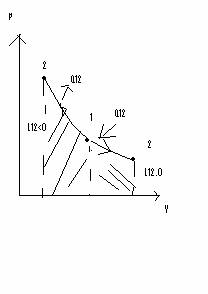
Transformarea adiabatia Q=0

pV=ct sau p1V1=p2V2=>TV la puterea k-1 = const =>T1V1 la k-1 = T2V2 la k-2

Ec. princip. intai devine

Q1, 2=DU1, 2+L1, 2=0

DU1, 2=-L1, 2=mC, DT=mVc(T2-T1)

L1, 2=p1V1-p2V2/k-1 = p1V1/k-1[1-(p2/p1) la k-1/k]

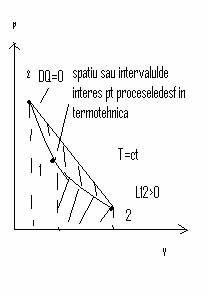
5. Transformarea politropica(generala)

pV la n – const

P1V1 la n = p2V2 la n TV la n -1 = ct T/p n-1/n=ct n apartine (-∞, +∞)

Pentru cazul masinilor si instalatilor termice prezinta interes transformarile politropice in care n apartine intervalului (1, k)

L1, 2=p1V1-p2V2/n-1 = mR(T1-T2)/n-1 = p1V1/n-1∙[1-(p2/p1) la n-1/n]

Q1, 2 = m δ U DT, unde Cn – caldura specinstalatii frigorificeica politropica

Din ecuatia pV la n = ct particularizam pe n

n=o => p – ct => trans izobara

n=1 => pV = ct => trans izotermica

n=K => pV la k = ct => trans adiabata

n=±∞ => trans izocora

Capitolul  4 Amestecul de gaz

In termotehnica prop. amestecului de gaze ideale se studiaza in urmatoarele ipoteze:

a)     Intre componentii sai intervin reactii chimice astfel incat compusii amestecului nu se modinstalatii frigorificeica

b)1 Fie gazele componente sunt raspandinte in intreg volum al amestecului deci fiecare gaz ocupa acelasi volum si are aceiasi temp ca si amestecul dar presiunile partiale ale comp sunt dinstalatii frigorificeerite(legea lui Dalon); in acest caz presiunea totala este egala cu suma presiunilor partilale ale gazelor componente.

P ameste = ∑pi componente

b)2 Fie gazele componente se considera separate prin peretii imaginari in fiecare caz avand aceeasi presiune si temeperatura si amestecul lui dar volumele lor partiale fiind dinstalatii frigorificeererite (legea lui Amagat). In acest caz volumul ocupat de amestecul de gaze este egal cu suma volumelor partiale ocupate de gazele componente

Vamestec = ∑Vi component

k=γ= Cv/Cp=i+2/i

i= este nr gradelor de libertate ale moleculelor

i=3 – pt gaz ideal monoatomic

i=5 – pt gaz ideal biatmoic

i=6 – pt gaz ideal poliatomic