METODE GEODEZICE DE MASURARE A VECTORILOR DEFORMATIILOR ORIZONTALE SI ALE DEPLASARILOR CONSTRUCTIILOR

METODE GEODEZICE DE MASURARE A VECTORILOR DEFORMATIILOR ORIZONTALE SI ALE DEPLASARILOR CONSTRUCTIILOR

Prin prelucrarea masurarilor liniare si unghiulare, se va putea obtine fie direct marimea vectorului deplasarii orizontale, fie mai intai marimile componentelor pe axele de coordonate si apoi, in functie de acestea, marimea vectorului deplasarii.

Vectorul deplasarii orizontale se poate determina prin metode grafice, metode numerice (trigonometrice, analitice) si metode riguroase, folosind metoda celor mai mici patrate, in functie de natura si precizia cercetarii.

1. Metoda trigonometrica - microtriangulatia

Se foloseste la determinarea vectorului deplasarii orizontale ale punctelor de control, fixate pe constructia luata in studiu, in raport cu un sistem de referinta, constituit din puncte fixate in terenuri nedeformabile si in afara zonei de influenta a constructiei, formind reteaua punctelor de microtriangulatie.

Metoda microtriangualtiei este folosita la urmarirea comportarii in timp a constructiilor masive (baraje, ecluze, viaducte, poduri), ca si a terenurilor din jurul acestora. Constructia retelei de microtriangulatie se face cu o precizie mare.

Determinarea vectorului deplasarii orizontale a constructiei necesita efectuarea masurarilor repetate (ciclice) ale retelei de microtriangulatie, cu aceeasi precizie cu care a fost construita initial. Calculele de compensare trebuie executate riguros, prin metoda celor mai mici patrate, cu scopul de a se obtine valorile cele mai probabile ale coordonatelor punctelor retelei, avindu-se posibilitatea aprecierii preciziei rezultatelor compensarii si deci, si a preciziei de determinare a vectorului deplasarii orizontale a punctelor de control, de pe constructia studiata.

In figura anterioara se prezinta reteaua de microtriangulatie folosita la urmarirea comportarii unui baraj arcuit. In componenta retelei intra urmatoarele categorii de puncte:

- puncte de control, numite si marci de vizare, ce sunt nxaie pe constructii ce lirniea^a *1 observata, (sri ca;',ui tic laia sunt incastrate in parainentul aval al barajului), .Aceste puncte, Pi, F"..-,Pt" au roiul de a da cu exactitate marimile si directiile deplasarilor. Semnalizarea lor se face cu marci speciale de diferite forme, confectionate din bronz cromat spre a rezista la coroziune. Cercetarile au aratat ca cele mai bune sint semnalele sub forma de disc, diametrul cercului j reprezentind 1:20 din distanta medie de la punctul fix la punctul de determinat. De exemplu, la o distanta de 400 m diametrul cercului va fi de 20 mm. Aceasta forma corespunde atit cazului vizelor orizontale, cit si al vizelor inclinate.

In aceasta figura s-a notat cu (1) - marca de vizare, (2) - piesa metalica de protectie, (3) -beton simplu pentru fixarea marcii, (4) - elementul de constructie in care este fixata marca;

- puncte de statie, din care se fac observatii repetate spre punctele de control de pe constructie. Punctele de statie, de exemplu I, II, III si IV, sunt materializate prin pilastri de beton armat, cu fundatie adanca, avand la partea superioara piese speciale de centrare si prindere a teodolitului.

In aceste figure s-a notat cu: (1) - dispozitivul decentrare fortata; (2) - capacul de protectie;(3) - beton simplu de fixare a dispozitivului si (4) - elementul de constructie, adica partea superioara a pilastrului.    Ele sunt amplasate in apropierea constructiei, la maximum 300500 m, numarul lor fiind de cel putin doua.

La o serie de cercetari, la partea superioara a pilastrului s-a fixat, in beton, o placa de otel in mijlocul careia se afla dispus un reper cu filet ce inlocuieste surubul pompa. Astfel se asigura o perfecta centrare a teodolitului si a semnalelor de vizare pe punctele de statie;

- punctele de referinta, K₁, K₂, K₃, de la care se determina eventualele schimbari in pozitia punctelor de statie sint amplasate in terenuri stabile si la distante de 200300 m de constructia observata, spre a se elimina orice influenta a acesteia asupra lor;

- punctele de orientare O₁, O₂, O₃, amplasate la distante mai mari, in terenuri care prezinta un grad ridicat in privinta stabilitatii, indicate de studiile geotehnice.

Reteaua de microtriangulatie se poate prezenta sub una din urmatoarele tipuri:

- retea completa, care cuprinde toate cele patru categorii de puncte si cu vize reciproce intre punctele de statie si punctele de referinta;

statie si punctele de referinta;

- retea superficiala, compusa din puncte de statie si puncte de referinta. La realizarea retelei de microtriangulatie se urmareste obtinerea unei bune conformatii a figurilor geometrice componente, in vederea obtinerii unei precizii antecalculate care sa satisfaca pe deplin cerintelor impuse. Se alege un sistem de axe rectangular care sa coincida cu axele principale ale constructiei observate. De exemplu, in cazul urmaririi comportarii unui baraj, deformatiile rezultate pe axa Y, paralela cu axa barajului, sunt mai mici decat cele pe verticala, adica dupa axa Z, care la randul lor sunt mai mici decat cele paralele directiei presiunii apei, adica dupa axa X.

In general, se masoara doua baze, cu precizia de 1:200 000 1:600 000. Cercetarile facute in ultimele doua decenii au aratat insa, ca masurarea cu mare precizie a doua baze nu este justificata din punct de vedere economic si ca este suficienta masurarea unei singure baze cu o precizie de 1:1 000 1:5 000, a carei marime va ramane constanta pentru toate ciclurile de observatii. Deoarece precizia de masurare a laturilor, cand se masoara o singura baza, va fi in cel mai rau caz cu circa 7% mai mica decat in cazul cand se iau doua baze, rezulta ca existenta a doua baze de asemenea nu se justifica intrucat precizia de determinare a lungimilor laturilor creste fara importanta.

Observatiile in punctele retelei de microtriangulatie se executa cu precizia corespunzatoare retelelor de ordinul I, II . ..uneori chiar III, prin metoda seriilor complete (reiteratiilor) sau prin metoda Schieiher. in timpul masurarilor unghiulare se iau toate masurile pentru a se elimina complet influenta erorilor sistematice si pentru a se reduce la minimum influenta erorilor aleatoare.

La calculul deplasarilor orizontale ale constructiei, unghiurile, orientarile si coordonatele punctelor din ciclul initial de masurari devin, dupa compensare, elemente de referinta. Fata de acestea, se raporteaza toate elementele obtinute in ciclurile urmatoare de observatii.

Schimbarile in pozitia punctelor de control, de pe constructia studiata, se determina prin metoda intersectiei, pe cale trigonometrica, analitica sau prin metoda celor mai mici patrate. in fiecare ciclu de observatii se va verifica stabilitatea in pozitia punctelor de statie; in cazul deplasarii unora din ele, se va proceda la introducerea corectiilor corespunzatoare.

Procesul determinarii vectorului deplasarii orizontale a punctelor de control, de pe constructia studiata, cuprinde urmatoarele etape:

1. Etapa masurarilor unghiulare si liniare la locul experimentarii, in laborator sau

pe teren in fiecare ciclu de observatii si care cuprind:

- masurarea directiilor orizontale din toate punctele de statie si a distantelor;

- compensarea directiilor orizontale, masurate in fiecare punct de statie, prin metoda riguroasa a masurarilor indirecte sau, in cazul unor experimentari mai putin precise, prin metoda empirica;

- evaluarea preciziei masurarilor unghiulare si liniare;

- cercetarea stabilitatii punctelor de statie si calculul modificarilor in directiile punctelor observate.

2 Etapa prelucrarii datelor masurarilor, pentru calculul vectorului deplasarii constructiei si evaluarea preciziei, care cuprinde:

- testarea stabilitatii punctelor fixe in raport cu care se efectueaza masurarea vectorului deplasarii; daca se constata ca unele puncte fixe si-au modificat pozitia, se calculeaza marimile deplasarilor punctelor fixe, ca si directiile deplasarilor si se introduc corectiile corespunzatoare;

- calculul vectorului deplasarii orizontale, ale punctelor de control, de pe constructia studiata;

- evaluarea preciziei de determinare a vectorului deplasarii si stabilirea, pentru o probabilitate data, a intervalelor si domeniilor de incredere in care se afla;

- intocmirea documentatiei tehnice a cercetarii.

Modul de efectuare a masurarilor unghiulare si liniare, prelucrarea masurarilor, obtinerea valorilor definitive (compensate) ale marimilor masurate si evaluarea preciziei rezultatelor, nu vor fi prezentate in cadrai acestei lucrari, ele fiind in general cunoscute Sl prezentate pe larg in mai multe carti de specialitate. De aceea, in continuare .se vor prezenta doar aspectele legate strict de problemele geodeziei aplicate la studiul constructiilor.

1.1. Teste privind stabilitatea punctelor fixe folosite la masurarea vectorului deplasarii orizontale

In fiecare ciclu de observatii, una din problemele de cea mai mare importanta este verificarea conditiilor de stabilitate a pozitiei punctelor fixe, fata de care se raporteaza toate punctele de control incastrate pe constructie, in vederea determinarii vectorului deplasarii.

La masurarea deplasarilor orizontale ale constructiilor, reteaua geometrica a punctelor fixe se amplaseaza astfel incat .sa nu fie supusa influentei factorilor ce produc deplasarea si deformarea constructiei. Dar calitatea observatiilor este influentata in masura insemnata de erorile provocate de neluarea in consideratie a deplasarilor sistemului de referinta care se considera alcatuit din puncte fixe, ceea ce modifica rezultatele si influenteaza valoarea si precizia masurarilor.

Este necesar a se controla stabilitatea punctelor fixe, stiind ca uneori aceste puncte nu sunt stabile, ci sufera deplasari datorita unor cauze complexe. Deplasarea punctelor fixe din reteaua de referinta (de microtriangulatie) impune introducerea in calcul a unor corectii directiilor unghiulare, permitandu-se efectuarea corecta a calculelor necesare determinarii vectorului deplasarii punctelor de pe constructia supusa observatiilor

Determinarea stabilitatii punctelor de statie din reteaua de microtriangulatie se face cu ajutorul punctelor de referinta si a punctelor de orientare. Dovada stabilitatii punctului. de statie, intr-o anumita perioada de timp, in raport cu celelalte puncte acceptate ca stabile, va fi egalitatea unghiurilor masurate in statiile respective in fiecare ciclu de observatii, egalitate ce trebuie inteleasa cu anumite limite, date de erorile inerente de masurare.

Deplasarea punctelor fixe, din reteaua de microtriangulatie, impune introducerea in calcul a unor corectii directiilor masurate. Directiile noi, corectate prin aducerea lor la paralelism cu directiile ciclului initial de observatii, adica la pozitia nedeplasata, a punctelor fixe, permit efectuarea corecta a calculelor necesare determinarii vectorului deplasarii constructiei studiate.

Astfel, daca se considera pozitia initiala a unui punct de statie, A. din reteaua de referinta, din care se vizeaza un alt punct de referinta (sau de orientare) O_i si daca, dupa o anumita perioada de timp, punctul de statie se va deplasa din pozitia initiala, A, in pozitia actuala, A', rezulta necesitatea corectarii tuturor-datelor obtinute din statia deplasata, A', in functie de marimea deplasarii produse.

Comparandu-se valorile directiilor unghiulare, din punctul A spre punctul O_i rezultate din ciclul initial C_i si din ciclul actual, C_i', se observa ca trebuie sa se introduca corectia ei. in vederea realizarii paralelismului dintre cele doua directii. In sistemul de axe rectangulare pentru corectia ei, rezulta relatiile simplificate:

,

unde:

,

iar Dx si Dy sunt componentele pe axe ale deplasarii, e, a punctului de statie.

Pentru aprecierea stabilitatii, se compara valorile unghiulare obtinute din calcul cu o valoare limita, iar in caz de neincadrare in aceasta limita, se calculeaza valoarea liniara a deplasarii.

Notandu-se cu C_i directiile initiale, si cu C_i', directiile actuale, masurate din punctul de statie A catre punctele de referinta O₁, O₂, O₃, . .., O_i, . , O_n, se fac diferentele:

, (i=1, 2, . n)

In functie de erorile medii patratice ale directiilor unghiulare masurate in ciclul initial, μ, si in ciclul actual, μ', se calculeaza eroarea medie patratica a unei singure diferente unghiulare:

Se calculeaza diferenta medie din punctul de statie. A, respectiv:

,

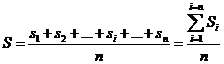si cu ajutorul acesteia se calculeaza abaterile diferentelor partiale, s_i, fata de diferenta medie S:

Eroarea medie patratica a unei singure diferente unghiulare, functie de abaterile fata de medie,este:

Pentru verificarea stabilitatii, se calculeaza:

,

a carei marime se compara cu o valoare admis, obtinindu-se indicatii daca punctul de statie s-a deplasat, adica

arata ca punctul este stabil, iar daca

arata ca punctul s-a deplasat si in concluzie, trebuie sa se calculeze corectiile directiilor.

In baza celor aratate mai sus, s-au propus mai multe teste de apreciere a stabilitatiipunctelor. Astfel, W.Lang, a propus un test simplu in functie de erorile medii patratice ale diferentelor partiale si a abaterilor fata de media aritmetica. Pe baza acestui test, inegalitatea indica:

- punct stabil

- punct deplasat

T.Lazzarini a propus un test mai complet exprimat de inegalitatea:

- punct stabil

- punct deplasat

unde:

in care n - numarul punctelor de referinta sau de orientare, iar t - numarul seriilor effectuate. Tot in cazul testului lui T.Lazzarini, cind raportul

,

atunci se poate aprecia ca punctul este stabil.

Utilizarea acestor teste prezinta dezavantajul ca deplasarile se exprima doar functie de elementele unghiulare, fara indicatii asupra elementelor liniare.

Eliminarea acestui dezavantaj se face prin folosirea testului de stabilitate elaborat de B.Ney.

In cadrul acestui test se stabileste dependenta abaterii liniare functie de diferenta unghiurilor orizontale masurate. In punctul de statie, A, s-au masurat directiile orizontale.

Determinarea deplasarii liniare, functie de diferentele unghiurilor orizontale masurate in punctul de statie, se face din cite doua combinatii, in raport cu numarul punctelor de referinta vizate, in total din r determinari calculate cu relatia:

Unghiurile orizontale masurate in cele doua cicluri de observatii, bj si b'j, sint afectate -z rr?n merente de masurare, iar diferentele dintre ele

cuprind atit erori de masurare cit si influenta deplasarii punctului de statie din pozitia A in A'.

Pe baza erorilor medii patratice ale directiilor masurate in cele doua cicluri de observatii, se calculeaza erorile medii patratice ale unghiurilor orizontale , adica:

,

si admitandu-se ca , se obtine pentru eroarea medie patratica a diferentei unghiurilor orizontale, expresia:

De asemenea, se calculeaza eroarea medie patratica a diferentei unghiurilor masurate si in functie de diferentele (abaterile) dintre valorile actuale si valorile initiale ale unghiurilor compensate:

Se face calculul deplasarii liniare a punctului de statie, din pozitia A in politia A', in functie de lungimile directiilor si a unghiurilor dintre ele, corespunzator celor r combinatii, cu formula:

,

in care:

In relatiile de mai sus, indicele i ,se refera la punctul de statie A_i. Raportul este constant, iar coeficientul K_i poate ti considerat ca parametru al punctului A_i, din reteaua de referinta, fiind de asemenea constant pentru toate ciclurile de observatii; precizia de determinare a elementelor ce intra in calculul acesteia trebuie sa fie de 1:200 1:500.

Evaluarea finala a marimii deplasarii liniare, e_i, se face dupa luarea in consideratie a nesigurantei pe care o contine, data de determinarile independente din fiecare combinatie. Determinarea acestei nesigurante este identica cu determinarea erorii medii patratice a marimii, e_i, care se obtine cu relatia:

Cu ajutorul acestei relatii s-a stabilit un criteriu exprimat de inegalitatea

- indica punct stabil,

unde eroarea medie admisa .

Aplicindu-se principiile statisticii matematice, considerindu-se ca valorile marimilor, e_i, au o distributie normala, se obtine:

unde - coeficient de amplificare a carei valoare depinde de numarul masurarilor si de marimea probabilitatii; - eroare limita.

In acest fel se mareste gradul de nesiguranta, , ceea ce corespunde cerintelor practice. Criteriul stabilitatii punctului de statie, in intervalul de timp dintre ciclurile de observatii, initial si final, devine:

,

implinirea inegalitatii, indicind stabilitatea punctului de statie.

S-a studiat, pe cale experimentala (simulata), deplasarile punctului de statie folosind testele W.Lang, T.Lazzarini si B.Ney. Rezultatele au aratat ca cea mai apropiata de valoarea cea mai probabila a deplasarii este cea calculata prin metoda B.Ney.

1. Calculul corectiilor directiilor masurate in punctele de statie deplasate

Deplasarile punctelor de statie si a celor de referinta se pot determina prin metode grafice, grafo-numerice si numerice.

Metoda numerica consta in urmatoarele:

Pe baza unghiurilor masurate se calculeaza componentele. Dx si Dy, ale deplasarii orizontale a punctului de statie A, in raport cu punctele fixe ale retelei de microtriangulatie O₁, O_2, O₃ (fig8.)

Din figura se observa ca:

si

Se calculeaza abaterile transversale ale punctului de statie deplasat, A', fata de directiile O₁A, O₂A si O₃A, cu relatiile:

,

,

,

si in fiinctie de acestea, unghiurile sub care se observa cele trei abateri:

, , ,

sau, in general,

,

unde: r^cc= 636620; p_i - abaterile transversale, exprimate in milimetri; D_i - distantele de la punctul de statie pina la punctul de referinta O_i, exprimate tot in milimetri.

Unghiurile orizontale masurate in ciclul actual, adica in punctul de statie deplasat, A', vor fi exprimate de formulele:

,

Aceleasi valori se obtin si din diferenta directiilor corectate. Astfel, directiile masurate in ciclul actual sint exprimate in functie de directiile masurate in ciclul initial

corectate cu marimile , de relatiile:

, ,

In cazul unei precizii mai reduse, calculul corectiilor unghiulare, , se poate

realiza mai repede prin metoda grafica.

Din analiza relatiei de calcul a erorii medii patratice a corectiei unghiulare

rezulta ca precizia de determinare a corectiilor unghiulare este invers proportionala cu distanta dintre puncte. Aceasta este explicatia recomandarii ca distanta dintre punctele de statie si punctele de referinta sa nu fie mai mare de 200300 m.

1.3. Determinarea vectorului deplasarii orizontale a constructiei studiate

Metodele de baza folosite la determinarea vectorului deplasarii constructiei sint metodele intersectiilor unghiulare si liniare, simple sau multiple, principial aceleasi ca cele folosite in geodezie si topografie, cu perfectionari de calcul potrivit specificului unor astfel de lucrari si caracterizate de o precizie superioara, atit in privinta masurarilor cit si al metodelor folosite.

In cazul metodei intersectiei unghiulare inainte simple, problema consta in determinarea vectorului deplasarii orizontale a punctelor de control, de pe constructia luata in studiu, in raport cu o baza de lungime fixa si de unghiurile orizontale masurate in punctele de statie, reprezentind capetele bazei, in ciclurile de observatii initial si actual.

In afara de rezolvarea trigonometrica clasica, de obtinere directa a marimii vectorului deplasarii, prezentata in literatura din tara noastra [146], dar foarte greoaie in privinta modului de conducere a calculelor, au fost date si alte rezolvari. Astfel, in tara noastra, Gr.Leoveanu folosind metoda punctului apropiat cu segmentele capabile [68], Gh.Nistor cu ajutorul dezvoltarilor in serie a diferentelor coordonatelor bipolare [86] si E.Popa prin diferentierea relatiilor de calcul a intersectiei inainte [116], au realizat noi posibilitati de calcul a deplasarilor, functie directa de diferentele masurate in diferite cicluri de observatii. De asemenea, folosind diferentierea relatiilor de calcul a intersectiei inainte, L.Novac si J.Strom au propus formule noi de calcul, pe care le-au folosit la masurarea deformatiilor constructiilor din panouri mari [108]. Pentru lucrari care necesita o precizie mai redusa, este cunoscuta metoda, devenita clasica, a constructiei grafice a lui W.Lang [146].

1.3.1. Metoda de determinare a vectorului deplasarii orizontale a constructiei functie directa de diferentele unghiurilor orizontale masurate ciclic din capetele unei baze fixe

Determinarea vectorului deplasarii orizontale a punctelor de control, fixate pe modele sau pe constructii la scara naturala, supusa la actiunea diferitelor solicitari, se poate executa cu ajutorul masuratorilor geodezice efectuate din punctele de capat ale unei baze de lungime fixa. in cele ce urmeaza, se analizeaza o metoda de determinare rapida, sigura si precisa a vectorului deplasarii orizontale a constructiei, elaborata de Gh.Nistor printr-o fundamentare matematica noua.

1.3.1.1. Stabilirea formulelor de calcul

Capetele bazei sint punctele de statie A si B, materializate prin pilastri de beton armat, amplasati in terenuri nedeformabile si in afara zonei de influenta a constructiei observate. Baza poate fi de sine statatoare sau poate face parte din reteaua de microtriangulatie, in functie de marimea si importanta constructiei ca si a naturii studiului efectuat (incercarea constructiei sau urmarirea comportarii in timp a constructiei). Deoarece se urmareste masurarea depla.sarilor punctelor de control si nu raportul fata de baza, nu este recomandabila marirea excesiva a preciziei de masurare a bazei, admitindu-se o precizie de 1:1000 1:5000.

Prin masurari ciclice, efectuate in punctele de statie, Asi B, asupra punctului de control, P, se determina componentele vectorului deplasarii orizontale (fig. 9).

Se alege un sistem rectangular de axe astfel ca punctul de statie A, sa fie originea sistemului, iar axa y sa corespunda cu baza AB. Pentru determinarea pozitiei plane a punctului de control, P, de pe constructia luata in studiu, se masoara, pe cale directa sau indirecta, lungimea bazei AB = b si unghiurile orizontale a si b

Fig. 9

in ciclul inifial de observatii, coordonatele bipolare ale punctului de control, P, sint exprimate de relatiile:

,

Datorita diferitelor solicitari, punctul de control, P, se deplaseaza impreuna cu constructia, in plan orizontal, in unul din punctele P₁, P₂, P₃ sau P_4. In cazul deplasarii punctului de control din pozitia P in P₁, in ciclul actual de observatii se masoara unghiurile orizontale a₁ si b₁. Deoarece s-a admis ca baza ramane fixa, coordonatele bipolare ale punctului deplasat, P_1, vor fi:

,

Componentele vectorului deplasarii orizontale a punctului de control, pe cele doua a.xe, vor fi:

,

Acest mod de determinare este foarte dificil. Din aceasta cauza, plecindu-se de la pnncipiul folosit si de alti autori, de determinare a componentelor deplasarii in functie directa de diferentele unghiurilor orizontale, s-au exprimat unghiurile orizontale, masurate in ciclul actual, in functie de valorile masurate in ciclul initial:

,

Componentele deplasarii punctului de control, din pozitia P in P₁ vor fi:

,

Deplasarile orizontale ale constructiilor fiind suficient de mici, inseamna ca si diferentele unghiulare Da si Dbsint mici; in relatiile de mai sus, tangentele sumelor de unghiuri se vor putea scrie sub forma:

Facindu-se inlocuirile de forma in relatii, dupa o serie de transformari in care s-au neglijat termenii continind cresterile de ordinul trei, formulele componentelor devin:

unde s-a notat cu:

Analog se obtine:

unde s-a notat cu:

Formulele de calcul nu sint practice, din care cauza, au fost dezvoltate in serie Mac Laurin obtinindu-se:

In relatiile de mai sus, influenta ultimilor doi termeni din paranteze este neglijabila,

din cauza micimii termenilor si , astfel incit, pentru componentele deplasarii se pot scrie relatiile:

,

dupa care, inlocuindu-se A, B, A₁, B₁, si M cu valorile lor, va rezulta:

,

Precizia impusa la determinarea prin masurari a parametrilor constructiei studiate a condus la inlocuirea in expresiile de mai sus, a functiei tangenta, cu functiile sinus si cosinus, obtinindu-se pentru componentele vectorului deplasarii orizontale formulele:

,

In relatiile de mai sus, facindu-se notatiile:

rezulta pentru componentele vectorului deplasarii orizontale a punctului de control, din pozitia initiala , in pozitia actuala, formulele definitive:

,

.

Aceste formule, de o deosebita simplitate, exprima direct marimile componentelor vectorului deplasarii orizontale a punctului de control, de pe constructia observata, in functie de diferentele dintre unghiurile orizontale masurate in cele doua cicluri de observatii.

Relatiile au caracter de generalitate, fiind valabile pentru calculul componentelor deplasarii punctului de control, P, in oricare din pozitiile P₁, P₂, P₃ sau P₄, diferentele unghiulare intrind in calcul cu semnele respective. Marimile K₁, L₁, K₂, L₂, sint calculate cu elementele masurate in ciclul initial si ramin constante pentru toate ciclurile de observatii ulterioare. Elementele ce difera de la un ciclu la altul sint doar diterentcie unghiulare Da­^ccsi Dab^cc ale caror marimi se exprima direct in secunde intrucit. in calculul constantelor a fost introdus si modulul de transformare a gradelor in radiani (r^cc= 636 620 sau r'= 206 265).

Marimea vectorului deplasarii orizontale a punctului de control, functie de manm:lr componentelor pe cele doua axe, este:

Orientarea vectorului deplasarii orizontale, fata de axa X, este data de relatia:

Metoda prezentata este mai rapida chiar decit metoda grafica, avind avantajul asigurarii unei precizii proprii metodelor numerice.

1.3.1. Evaluarea preciziei de determinare a vectorului deplasarii orizontale prin metoda propusa

Componentele vectorului deplasarii orizontale a constructiei studiate sint functii de marimile indepenente b, a si b, precum si de diferentele unghiulare Da si Db, care pentru simplificare, se vor considera tot ca marimi independente.

Pentru calculul erorilor medii patratice ale componentelor vectorului deplasam foloseste:

Calculindu-se derivatele partiale si notindu-se ctg(a+b) = ctg(200^g-γ), se obtin formulele de calcul a erorilor medii patratice ale componentelor vectorului deplasarii orizontale:

In relatiile obtinute, marimilesi nu se mai impart la ρ² deoarece acest termen este cuprins in calculul patratelor constantelor, K²₁, L²_1, K²₂ si L²

Erorile medii patratice ale componentelor vectorului deplasarii corespund cazului general, cind precizia de masurare a unghiurilor orizontale, in cele doua cicluri de observatii, este diferita astfel incat:

,

erorile medii patratice ale diferentelor unghiurilor fiind date de relatiile:

,

Pentru cazul in care unghiurile orizontale s-au masurat cu aceeasi precizie, inseamna ca:

si

,

iar formulele ce exprima erorile medii patratice ale componentelor vectorului deplasarii devin:

Indiferent de precizia de masurare a unghiurilor orizontale eroarea medie patratica a vectorului deplasarii este data de relatia:

Deoarece, asa cum s-a mai aratat, marimile K₁, L₁, K₂, L₂, sint determinate cu elementele masurate in ciclul initial si ramin constante pentru toate ciclurile de observatii ulterioare, se va analiza marimea erorii medii patratice a vectorului deplasarii constructiei, functie de marimile masurate Da si Db, celelalte marimi considerindu-se constante. in acest caz, marimea erorii medii patratice a vectorului deplasarii orizontale va fi:

,

iar dupa calculul derivatelor partiale ale vectorului L, in raport cu variabilele Da si Db, pentru cazul in care , va rezulta:

Cand unghiurile orizontale s-au masurat cu aceeasi precizie, inseamna ca , iar formula erorii medii patratice a vectoruluideplasarii devine:

,

Pentru analiia conditiilor optime de determinare a vectorului deplasarii este necesara stabilirea dependentei erorii vectorului fata de marimea unghiului, γ, sub care se intersecteaza dreptele de determinare.

Fata de cazul general de determinare, se analizeaza cazul particular cind unghiurile orizontale, ca si lungimile dreptelor de determinare, sint aproximativ egale:

,

iar eroarea vectorului deplasarii devine :

Pentru cazul particular analizat, rezulta unnatoarele relatii evidente:

, , cu observatia

care va conduce la expresia erorii medii patratice a vectorului deplasarii in functie de unghiul sub care se intersecteaza dreptele de determinare si de marimea acestora.

Analiza relatiei obtinute arata ca eroarea medie patratica a vectorului deplasarii este direct proportionala cu distanta de la punctele de statie la punctele de control si cu eroarea medie patratica a diferentelor unghiulare si invers proportionala cu marimea vectorului deplasarii precum si cu sinusul unghiurilor sub care se intersecteaza dreptele de determinare.

La evaluarea preciziei rezultatelor trebuie calculate marimile relative si absolute ale erorilor.

Se obtine pentru eroarea medie patratica relativa expresia:

Eroarea medie patratica absoluta se obtine prin exprimarea erorii vectorului deplasarii orizontale a constructiei in functie de lungimea bazei fixe. Pentru aceasta se face substitutia:

obtinind pentru eroarea medie patratica absoluta relatia:

Cercetarile efectuate au aratat ca valorile obtinute pentru eroarea medie patratica a vectorului deplasarii, fie functie de erorile componentelor, fie direct sunt sensibil egale. Aceasta demonstreaza ca precizia diferentelor unghiurilor si deci precizia masurarii unghiurilor orizontale, in toate ciclurile de observatii, are influenta cea mai mare asupra preciziei de determinare a vectorului deplasarii.

Trebuie aratat ca, marimile erorilor medii patratice, si , ale componentelor vectorului deplasarii punctului de control, reprezinta abaterile vectorului determinat pe directiile axelor de coordonate. In timp ce si pot avea semnul plus sau minus, eroarea totala este esential pozitiva. In functie de marimea lui este imposibil sa se determine valorile abaterilor vectorului relativ si la alte directii si sa se studieze in ce directie aceste abateri au valori maxime sau minime. Marimea lui furnizeaza limite prea largi pentru aprecierea vectorului deplasarii constructiei. Acest aspect se pune in evidenta foarte clar cind, pentru aceeasi marime a lui m,, erorile si difera mult ca marime. Astfel, descriindu-se un cerc injurai punctului de control, P, (figura 10) se construieste dreptunghiul ABCD care este determinat de erorile medii patratice si . Dar dimensiunile laturilor acestui dreptunghi, deci si raportul marimilor si ., se pot schimba foarte mult (de exemplu dreptunghiul A₁,B₁,C₁,D₁,), iar marimea lui ramine aceeasi.

Asfel se poate trage concluzia ca eroarea medie patratica nu poate caracteriza safisfacator precizia in determinarea vectorului deplasarii.

O idee completa si clara asupra preciziei vectorului deplasarii o da elipsa erorilor.

Marimile semiaxelor si orientarea elipsei erorilor depinde de marimea unghiului sub care se intersecteaza dreptele de determinare si de lungimile acestor drepte. in practica, elementele elipsei erorilor vectorului deplasarii constructiei, sint exprimate de relatiile :

Ultima ecuatie are doua radacini: 2Ѳ si 2Ѳ ± 200^g adica Ѳ si Ѳ ± 100^g astfel ca

Fig. 11

ele determina doua directii perpendiculare care vorcorespunde celei mai mari si celei mai mici abateri ale vectorului deplasarii, respectiv axelor principale ale elipsei erorilor (fig.11).

Mai corect, trebuie spus ca precizia vectorului deplasarii este data de curba pedala sau curba erorilor medii patratice, care se defineste ca locul geometric al picioarelor perpendicularelor duse din centrul elipsei pe tangentele la elipsa si a carei ecuatie este:

unde: f - unghiul dintre semiaxa mare si raza vector R, luat in sens direct acelor unui ceasornic.

Pe baza constructiei curbei pedala, se pot determina erorile medii patratice ale jctorului deplasarii, pe cele doua axe, si , prin masurarea segmentelor

,

Pe aceeasi figura s-au mai facut notatiile:

, ,

Pentru cazul simplifactor in care , deci si , relatiile elementelor elipsei erorilor capata forma:

,

,

.

Din ultima egalitate rezulta ca Θ1=0g si Θ2=100g se deduce ca, in acest caz ca axele elipsei erorilor coincid cu axele de coordonate. Efectuindu-se raportul dintre patratele semiaxelor elipsei erorilor se obtine:

, de unde

Conform acestei relatii, cind γ=100^g, raportul semiaxelor este egal cu unitatea ti deci, A = B; elipsa erorilor degenereaza intr-un cerc al erorilor. Aceeasi relatie da indicatii asupra formei elipsei erorilor, astfel:

- pentru γ < 100^g rezulta ca A> B,

- pentru γ > 100^g rezulta ca A < B .

De asemenea, pentru valori ale unghiurilor γ, egale cu 60° si 120° , semiaxa marc este mai mare ca semiaxa mica de 1,73 ori, dar pozitia elipsei este diferita. In primul caz, semiaxa mare este dirijata pe bisectoarea unghiului γ, iar in al doilea, este paralela cu baza de lungime fixa, AB. O reprezentare evidenta a dimensiunilor si formei elipsei erorilor pentru diferite valori ale unghiului γ sint date in figura urmatoare:

Indicatii asupra dimensiunilor elip.sei erorilor sint date fie de ponderea elipsei erorilor exprimata de relatia:

,

fie de marimea suprafetei elipsei erorilor, data de formula:

Marimea preciziei de determinare a vectorului deplasarii constructiei este direct proportionala cu marimea ponderei si invers proportionala cu marimea suprafetei elipsei erorilor. Cu cit semiaxele elipsei erorilor sint mai mici, cu atit suprafata va fi mai mica iar ponderea, si deci si precizia, va fi mai mare.

La aprecierea preciziei vectorului deplasarii se va avea in vedere atit valoarea relativa cit si valoarea absoluta a suprafetei elipsei erorilor.

Suprafata elipsei erorilor se obtine prin inlocuirea valorilor semiaxelor:

Valoarea relativa a suprafetei elipsei erorilor in raport cu suprafata cercului de raza, d, se exprima prin relatia:

Valoarea absoluta a suprafetei elipsei erorilor se obtine prin inlocuirea marimii d, exprimata de formula:

Valorile absolute ale suprafetei elipselor, pentru diferite valori al unghiului

γ, sint reprezentate in figura 1

Cunoasterea elementelor elipsei erorilor (A, B, Θ, P sau S_e) da posibilitatea cunoasterii directiilor de-a lungul carora erorile vectorului deplasarii sint maxime si minime si domeniul de eroare, permitind alegerea anticipata a pozitiei si lungimii bazei de observare astfel ca erorile sa fie cele mai mici.

1.3.1.3. Conditii optime de determinare a vectorului deplasarii orizontale a constructiilor studiate

Pentru stabilirea conditiilor optime de determmare a vectorului deplasarii orizontale pnn metoda propusa, se prezinta un studiu amanuntit asupra optimului atit din punct de vedere al erorilor medii patratice cit si al elipselor erorilor.

Spre deosebire de cazul determinarii unui punct prin intersectia unghiulara inainte simpla sau multipla, folosit in topografie si geodezie, unde optimul se obtine prin studirea minimului erorii medii patratice in pozitia punctului determinat, in cazul determinarii vectorului deplasarii orizontale a constructiei observate acest lucru nu mai este posibil deoarece eroarea medie patratica depinde, in primul rand, de pozitia vectorului deplasarii fata de sistemul rectangular de axe.

In cele ce urmeaza, se analizeaza trei situatii caracteristice, determinate de pozitia vectorului deplasarii orizontale in raport cu sistemul de axe.

1. Vectorul deplasarii orizontale L₁, paralel cu axa x adica:

DX = L₁ si DY = 0

Substituindu-se rezulta pentru eroarea medie patratica relativa expresia:

Problema consta in determinarea unghiului dintre dreptele de determinare pentru ca eroarea sa fie minima. Rezulta ca:

cand , adica

Deci, minimul erorii relative se obtine daca γ = 200^g. Substituindu-se, rezulta pentru eroarea medie patratica absoluta expresia:

Minimul erorii absolute se obtine cind:

,

deci pentru γ = 200^g

Vectorul deplasarii orizontale L₂ paralel cu axa y, respective:

DX = 0    si Dy = L₂

Inlocuind in relatiile anterioare, se obtine pentru eroarea relativa expresia:

Rezulta ca:

cand ,

adica pentru γ=0^g.

3. Vectorul deplasarii este indreptat pe directia bisectoarei sistemului rectangular de axe, adica:

DX = DY si

Se inlocuieste si se obtine formula erorii patratice relative:

Minimul erorii absolute se obtine atunci cand

, adica pentru

Anularea derivatei da ecuatia:

, are loc maxim in intervalul pentru:

,

respectiv γ/2 = 60^g82^c sau γ= 121^g4^c.

Pentru functiile care reprezinta erorile relative ale vectorului deplasarii s-a intocmit tabelele de mai jos:

Analiza datelor din cele doua tabele duce la concluzia ca atit in cazul erorilor relative, cit si al erorilor absolute, cind dreptele de determinare se intersecteaza sub un unghi drept, eroarea medie patratica este aceeasi, indiferent de pozitia vectorului deplasarii orizontale a constructiei studiate, in raport cu axele de coordonate.

Pentru valori ale unghiului sub care se intersecteaza dreptele de determinare, adica pentru , s-au constniit graficele din figurile de mai jos ale marimilor erorilor relative si respectiv, absolute.

Din prima figura rezulta ca graficele erorilor relative si ale vectorilor deplasarii orizontale dispusi pe directiile axelor de coordonate, sint asezate simetric fata de abscisa care trece prin ordonata corespunzatoare lui γ = 100^g. Ele prezinta cite un punct de minim pentru γ = 200^g si respectiv γ = 0^g si au fiecare asimptota verticala.

Fig. 13 Fig. 14

Erorile devin egale cind γ = 100^g. Curba corespunzatoare erorii relative a vectomlui deplasarii orizontale, dispus pe directia bisectoarei sistemului de axe, are un minim pentru γ = 100^g si doua asimptote verticale, la γ = 0^g si γ = 200^g fiind de asemenea simetrica in raport cu aceeasi axa ca si primele doua.

In cea de-a doua figura sint reprezentate graficele erorilor absolute. Curba erorii absolute, , corespunzatoare vectorului deplasarii orizontale, cind acesta este dispus paralel cu axa X, are minim pentru γ = 200^g si tinde asimptotic spre axa absciselor. Curba reprezentativa a erorii, , care corespunde vectorului deplasarii, dispus paralel cu axa Y, are minim pentni γ = 100^g, e simetrica in raport cu paralela la axa absciselor care trece prin acest punct de nunim si prezinta doua asimptote verticale. In sfirsit, curba erorii absolute , corespunzatoare vectorului deplasarii, dispus pe directia bisectoarei sistemului de axe, are un minim pentru γ 120^g (mai precis γ = 121^g64^c), prezinta doua asimptote verticale, dar nu mai are elemente de simetrie. Si in cazul erorilor absolute, se constata ca pentru γ = 100^g curbele au un punct comun, deci aici marimile acestor erori devin egale.

Deoarece erorile medii patratice nu pot caracteriza in mod satisfacator precizia de determinare a vectorului deplasarii, se vor analiza conditiile optime si din punctul de vedere al elipsei erorilor.

Analiza relatiilor arata ca in cazul in care , deci si , rezulta urmatoarele relatii evidente:

, , ,

si de asemenea

, , ,

aceasta dearece, pentru cazul considerat, axele elipsei erorilor coincid cu axele sistemului rectangular in raport cu care se face determinarea vectorului deplasarii.

Conditiile optime de detreminare a vectorului deplasarii orizontale a constructiei studiate, din punctual de vedere al suprafetei elipsei erorilor, se stabilesc prin analiza minimului valorii relative si a valorii absolute a suprafetei elipsei.

Valoarea relative a suprafetei elipsei erorilor in raport cu suprafata cercului de raza d, va fi cea mai mica pentru cazul cand unghiul dintre dreptele de determinare va fi drept(γ = 100^g).

Pentru o lungime data, b, a bazei in raport cu care se efectueaza masuratorille, valoarea cea mai mica a suprafetei elipsei erorilor (valoarea absoluta), va corespunde valorii:

Prin logaritmare rezulta:

Maximul functiei U se va obtine pentru:

Aceasta ecuatie admite solutia:

si deci

Inlocuindu-se aceasta valoare a lui γ in derivata a doua:

rezulta ca aceasta este negativa si deci functia U(γ) va fi maxima pentru , iar valoarea absoluta a suprafetei elipsei erorilor va fi minima.

Pentru elementele relative si elementele absolute ale elipsei erorilor s-au intocmit tabelele urmatoare:

Analiza primului tabel si a figurii arata ca graficele valorilor relative ale elementelor elipsei vectorului deplasarii sint similare cu cele ale erorilor relative si prezinta aceleasi caracteristici. La fel, din analiza celui de-al doilea tabelsi a figurii    se poate trage concluzia ca graficele valorilor absolute ale elementelor elipselor erorilor sint similare cu cele ale erorilor absolute si prezinta aceleasi caracteristici cu o singura deosebire si anume aceea ca, daca minimul lui M^, se produce pentru valoarea lui γ = 120^g64^c minimul suprafetei elipsei erorilor, S_e, are loc pentru γ = 133^g34^c.

In incheierea acestui studiu se pot trage urmatoarele concluzii importante

- Cunoasterea conditiilor optime in care se pot face determinarile deplasarii r constructiilor supuse actiunii unor forte orizontale este de mare importanta in slabilir..--apriori a preciziei cu care se va obtine marimea vectonilui deplasarii orizontale.

- Atunci cind este posibila cunoasterea anticipata a directiei vectorului deplasarii orizontale, baza din capetele careia se fac inasurarile asupra punctelor de control de peconstructia observata trebuie astfel aleasa incit unghiul dintre dreptele de determinare sa conduca la erori medii patratice minime. Astfel, la determinarea vectonilui deplasarii orizontale a unui baraj, produs de presiunea apei din lacul de acumulare, baza se va alege paralela cu axa longitudinala a barajului si de o lungime astfel incit unghiul dintre dreptele de determinare sa fie apropiat de 200^g, valoare pentru care atit valorile relative. cit si valorile absolute ale erorilor medii patratice ale vectorului, devin minime. Alegerea celor mai optime conditii de determinare se poate face in cazul incercarii constructiilor pe modele si la scara naturala, unde solicitarile fiind dirijate, se pot anticipa cu precizie directiile deplasarilor rezultate.

- Cind nu este posibila cunoasterea anticipata a directiei vectorului deplasarii orizontale, se recmanda alegerea bazei astfel incat unghiul dintre dreptele de deteremnare sa fie aproximativ drept, deoarece pentru acest caz, valorile relative ca si cele absolute ale erorilor medii patratice sunt egale, idiferent de pozitia vectorului deplasarii.

- Chiar si in cazul respectarii conditiilor optim de determinare a vectorului deplasarii constructiei, influenta hotaratoare o are precizia diferentelor unghurilor orizontale, reprezentata de erorile medii patratice si , care depind de erorile medii patratice de masurare a directiilor si unghiurilor in cele doua cicluri de observatii, initial si actual.

- Nerespectarea conditiilor optime poate duce la situatia in care erorile metodei sunt cu mult superioare marimilor ce trebuie puse in evidenta prin masurare, aceasta ducand la concluzii eronate asupra constructiei studiate, cu repercusiuni grave asupra exploatarii in conditii de deplina securitate.

1.3. Metoda de determinare a vectorului deplasarii constructiei prin intersectie unghiulara inainte, simplificata

Metoda analitica a intersectiei unghiulare inainte simplificata se bazeaza pe exprimarea necunoscutelor reprezentate de componentele vectorului deplasarii ca functii liniare de termenii liberi. Simplificarea, datorata lui T.Lazzarini, consta in egalarea cu zero a relatiilor de erori, fara a influenta prea mult precizia de determinare a vectorului deplasarii.

Fig. 25

Exprimarea componentelor vectorului deplasarii orizontale a constructiei observate, functie directa de diferentele unghiurilor orizontale masurate in cele doua cicluri de observatii, se face prin relatiile de erori simplificate

unde:

Prin rezolvarea sistemului de ecuatii se obtin componentele vcctorului deplasarii

,

1.3.3 Metoda de determinare a vectorului deplasarii constructiei prin intersectie unghiulara inapoi, simplificata

Este considerata ca cea mai utila metoda de determinare a deplasarii punctelor fixe. de statie si de referinta, din reteaua de microtriangulatie, precum si a punctelor situate in zona terenurilor alunecatoare din regiunile muntoase si de pe malurile riurilor. Dar poate fi tot atit de utila si la masurarea vectorului deplasarii constructiilor mari, in special a podurilor, viaductelor, etc. In acest caz, in punctul de control, P, situat pe constructie, se masoara unghiurile orizontale a si b la intervale corespunzatoare ciclurilor de observatie.

Componentele vectorului deplasarii orizontale, se calculeaza pe cale analitica functie directa de diferentele unghiurilor orizontale, din relatiile de erori simplificate.

unde:

Valorile coeficientilor de directie, (i = A,B,C), se calculeaza fie cu ajutorul tabelelor, fie cu ajutorul formulelor.

Prin rezolvarea sistemului de ecuatii se obtin formulele de calcul ale componentelor vectorului deplasarii constructiei:

,

Sl functie de acestea, se calculeaza marimea si directia vectorului deplasarii.

1.3.4. Metoda de determinare a vectorului deplasarii orizontale a constructiei prin masurari indirecte ponderate tratate riguros prin metoda celor mai mici patrate

La determinarea simultana a vectorului deplasarii orizontale a punctelor de control, de pe constructia luata in studiu, in raport cu o serie de puncte fixe din reteaua de microtriangulatie, cea mai acceptabila cale de urmat ar fi urmatoarea:

Cu coordonatele cunoscute ale punctelor din reteaua de referinta se compenseaza toate masurarile executate separat in fiecare ciclu de observatii, obtinindu-se de fiecare data coordonatele punctelor de control. Din analiza distributiei coordonatelor acestor puncte, obtinute in fiecare ciclu de observatii, se pot constata marimile depla.sarilor absolute, partiale si totale. Acest mod de rezolvare a problemei propuse, acceptat in mod firesc si care duce la rezultate din cele mai bune, este insa extrem de anevoios, necesitind un volum important de calcule.

Deoarece o serie de elemente ale operatiei de tratare a masurilor efectuate sint comune tuturor ciclurilor de observatii, in cele ce urmeaza se va expune o metoda de determinare a vectorului deplasarii constructiei functie directa de elementele masurate direct pe teren. Acest mod de rezolvare a preocupat mai multi cercetatori, importante contributii aducind T.Lazzarini, V.Kurtev si G.ZIatanov , A.K. Zaitev si V.G.Sobciuc , in tara noastra problema a fost abordata de M.Neamtu    si Gh.Nistor. Modul de tratare a masurarilor prin metoda celor mai mici patrate a cuprins atat cazul masuratprilor indirecte cit si cazul masuratorilor conditionate. In ambele cazuri, prin tratarea riguroasa a masuratorilor, se obtin cele mai probabile valori ale componentelor vectorului deplasarii fiecarui punct de control sl erorile medii patratice ale acestora.

Datorita conditiilor dificile in care se realizeaza urmarirea comportari in timp a constructiilor mari, supuse la difcritc solicitari, din punctele fixe ale retelei dc microtriangulatie, cea mai indicate metoda de tratare a masuratorilor, rezultate in diferite ciclcuri de observatii, este metoda masuratorilor indirecte.

1.3.5. Metoda de detenninare a vectorului deplasarii orizontale a constructiei prin masurari indirecte corelate

La studiul comportarii con.structiilor prin masurari indirecte ponderate, vectctorul deplasarii orizontale se determina pe baza variatiei unghiurilor orizontale masurate, iar punctele fixe ale retelei de microtriangulatie, in fiecare ciclu de observatii. Intrucat pc teren se masoara marimile directiilor si nu unghiurile, compensarea prin metoda masuratorilor indirecte, in conditiile in care se considera unghiurile orizontale ca marimi' independente, duce la obtinerea unor rezultate mai putin riguroase in sensul metodei celor mai mici patrate.

Obtinerea unor rezultate riguroase este posibila prin introducerea unor corelatii matematice. Pe baza teoriei compensarii masuratorilor corelate, elaborate de J.M..Tienstra, se poate ajunge la solutii unice, indiferent de metoda de compensare a observatiilor.