Torsorul de reducere - Cazurile de reducere

Torsorul de reducere - Cazurile de reducere

Fig. 3.22

Torsorul de reducere al unui sistem de forte poate furniza informatii despre efectul cumulat al acestuia asupra corpului pe care il actioneaza. Astfel, exista o tendinta de translatare a corpului dupa directia si in sensul de actiune ale rezultantei simultana cu o tendinta de rotire a corpului in jurul unei axe coliniare cu momentul rezultant (fig.3.22).

Fig.3.23 Fig.3.24

Din analiza torsorului de reducere se poate determina cel mai simplu sistem de forte, echivalent ca efect  cu sistemul dat. In functie de valorile rezultantei si momentului rezultant se evidentiaza urmatoarele cazuri de reducere ale unui sistem de forte:

Cazul 1 . Sistem de forte aflat in echilibru; corpul ramane in repaus sau continua o deplasare rectilinie si uniforma. Toate sistemele aflate in echilibru sunt echivalente intre ele.

Cazul 2 . Sistem echivalent cu un cuplu de forte (fig.3.23) actionand intr-un plan perpendicular pe directia momentului rezultant . Sistemul are ca efect numai rotirea corpului in jurul axei coliniare cu .

Cazul 3: . Sistem echivalent cu o forta unica, egala cu rezultanta , actionand chiar in punctul de reducere (fig.3.24).

Cazul 4 : . Se deosebesc situatiile:

Fig.3.25 Fig.3.26

a) . In acest caz si deci . Torsorul minimal este compus numai din . Sistemul este echivalent cu o forta unica, egala cu rezultanta, actionand pe axa centrala (fig.3.25). Efectul sistemului este de translatare a corpului in lungul axei centrale.

b) .   Sistemul este echivalent cu un torsor minimal compus dintr-o forta egala cu , actionand pe axa centrala si un cuplu de forte de moment , actionand intr-un plan perpendicular pe axa centrala (fig. 3.26). Efectul sistemului consta dintr-o translatare a corpului dupa directia axei centrale si dintr-o rotirea simultana a acestuia, analog unei miscari elicoidale.

De remarcat ca situatia descrisa pentru cazul 3 este o particularizare a cazului 4, a), axa centrala trecand chiar prin punctul de reducere.

Fig.3.27

Problema 3.1: Se da un sistem de forte aplicat unui paralelipiped avand trei muchii suprapuse axelor de coordonate ca in fig.3.27.

Date: ,

,

(momentul unui cuplu).

Cerute: –si ;

– echivalenta sistemului;

axa centrala

– reprezentarea grafica a elementelor

de reducere.

Rezolvare: Forta are proiectie numai pe axa Oz. Proiectiile fortelor si se gasesc utilizand relatia 3.4) dupa cum urmeaza:

Momentele fortelor fata de punctul O se calculeaza cu relatia (3.9).

; ;

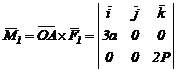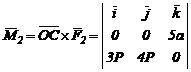Proiectiile fortelor si momentelor pe axele de coordonate, calculate cu aceste relatii, sunt concentrate in tabelul 3.1.

Tabelul 3.1

Fig.3.28

Ultima linie, obtinuta prin insumarea coloanelor, contine tocmai proiectiile pe axe ale rezultantei si momentului rezultant in urma reducerii in punctul O.

Modulul rezultantei, dat de rel.(3.42), are valoarea . Pentru torsorul de reducere in punctul D se calculeaza numai momentul rezultant. pornind de la in baza rel.(3.41). Se obtine astfel:

Componentele torsorului din punctul O si ale celui din punctul D sunt reprezentate in fig.3.28. Trinomul invariant al sistemului, definit prin rel.(3.44), are valoarea . Deoarece si ne aflam in cazul de reducere 4 b) analizat mai inainte. Sistemul dat este echivalent in consecinta cu un torsor minimal compus dintr-o forta egala cu rezultanta sistemului actionand pe axa centrala si dintr-un cuplu de moment minim.

Axa centrala se obtine facand inlocuirile in ecuatia generala (3.54

Rezulta imediat:

Momentul minim are valoarea

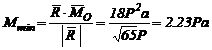
Axa centrala este o dreapta avand aceeasi directie cu rezultanta, situata intr-un plan paralel cu yOz. In fig.3.29 s-a reprezentat torsorul minimal care se obtine facand reducerea intr-un punct al acesteia.