Cauza si efect in economie - modelul unifactorial

CAUZA SI EFECT IN ECONOMIE - MODELUL UNIFACTORIAL

1. Relatiile de cauzalitate in economie si particularitatile lor

Situatiile in care un process economic depinde de un singur factor nu sunt prea frecvente in economie. Dintr-o perspectiva pedagogica este indicat sa incepem cu abordarea dependetei in raport de un singur factor, urmand astfel calea frecvent acceptata, de la simplu spre complex.

Daca am incerca sa desprindem din ansamblul relatiilor din economie acele relatii care implica un effect si un factor important, intr-o dependeta care ne asteptam sa fie de tip liniar, atunci am putea avea in vedere ca:

- cererea de alimente strict necesare depinde indeosebi de numarul populatiei;

productia, in conditiile in care utilajele sunt aceleasi, depinde de numarul de ore utilizate efectiv pentru realizarea ei;

- rata dobanzii la bancile comerciale, in conditii normale pe piata monetara, este influentata de rata dobanzii de referinta;

- exportul unui produs neschimbat din perspective calitatii, desfasurat in conditii relativ stabile privind cursul de schimb si conjuncture economica, depinde de nivelul pretului;

- productia de porumb, in conditii pedoclimatice neschimbate dar si in ce priveste calitatea semintei, este influentata de suprafata insamantata.

Retinem din toate aceste exemplificari cel putin 2 aspecte:

- faptul ca dependenta nu este "totala" intrucat intilnim mereu expresia "depinde de", aspectcare implica recunoasterea existentei si a altor cauze de o mai mica importanta sau prea putin cunoscute. Aceasta confera relatiei un character partial incert, aleator.

deseori e specificata existenta unor conditii care se mentin aceleasi, ceea ce poate fi valabil "in conditii de laborator", dar numai temporar poate fi constatat in viata reala pe un segment de cazuri. Asadar, dependenta unui proces in raport cu factorul determinant se poate manifesta diferit in decursul timpului, in raport cu gradul de stabilitate al celorlati factori importanti. La aceasta se adauga influenta elementului perturbator provocat de cauzele minore, putin cunoscute, mai mult sau mai putin accidentale.

Ca urmare a existentei unor astfel de particularitati in raport cu un singur factor, modelul prin care urmarim sa exprimam ceea ce consideram esential intr-un proces, trebuie sa includa:

- variabila-efect (notata cu , i=1,2,.,n);

- variabila cauzala (notata cu si uneori cu )

- relatia de tip liniar dintre variabila-efect si variabila cauzala:

(1

variabila care poate perturba relatia dintre principalii "actori", expresie a actiunii cauzelor minore, prea putin cunoscute, a caror influenta poate accentua sau diminua rolul factorului determinant. Acestor abateri, generate de astfel de cauze le rezervam, de asemenea, un loc in model, si anume le includem in partea dreapta a egalitatii sub forma unui termen (notat u, v sau e) care se insumeaza algebric la "cantitatea explicata" de factorul determinant. Ca urmare, modelul liniar unifactorial poate fi redat astfel:

(2

In model apar parametrii notati a, b (dar si sau ) care urmeaza sa fie determinati corespunzator datelor numerice ce privesc ansamblul (N) de cazuri sau urmeaza sa fie estimati daca datele se refera la un esantion (n) de cazuri.

Regresia statistica, estimarea parametrilor si semnificatia economica a acestora

Pentru a facilita intelegerea demersului econometric, dar si pentru a evidentia caracterul operational al modelului 2 abordim prezentarea metodei de estimare folosind un exemplu apropiat de procesele desfasurate in economia reala.

Astfel, daca avem in vedere prezumtia conform careia numarul populatiei (x) determina vanzarile unui produs de uz current (z), urmarim sa verificam realismul prezumtiei, dar si sa determinam cat mai riguros in ce masura modificarea numarului populatiei cu 1000 de locuitori provoaca modificari in ce priveste volumul vanzarilor. Datele de care dispunem se refera la 16 localitati (i=1,2,.,16) si sunt prezente in tabelul 1.

Tabelul 1

Reprezentate pe un system de axe (fig. 1) punctele de coordinate descriu un nor de puncte a carui forma urmeaza mai curand o dreapta decat o linie curba (polinom de gradul 2, exponentiala, hiperbola, etc)

Fig. 1

Intrucat reprezentarea ofera o imagine a imprastierii punctelor de coordonate , consideram graficul drept o diagrama a imprastierii (scatter diagrame). Faptul ca norul de puncte este alungit in asa fel incat poate fi redat intr-o forma stilizata printr-o linie dreapta, ne indreptateste sa acceptam drept model a relatiei de dependenta functia . Trasam astfel o linie in asa fel incat sa treaca prin mijlocul norului de puncte. Prelungirea dreptei spre stanga reprezentarii grafice intersecteaza axa Oy in punctual A - ceea ce semnaleata, dintr-o perspectiva geometrica, mirimea coeficientului "a". In raport cu fiecare dintre axe, dreapta se situeaza sub un unghi indicand panta - adica ceea ce esprima parametrul "b".

De la fiecare dintre punctele pana la dreapta se constata existenta unor distante mai mici sau mai mari reprezentand abateri generale de acei factori considerati nesemnificativi, accidentali, avand in orice caz un rol perturbator. Daca notam distanta de la fiecare punct de coordinate pana la proiectia sa pe dreapta cu simbolul , atunci marimea abaterii (distantei) este data de diferenta:

(3

Ceea ce intereseaza cu deosebire in continuare este obtinerea de solutii pentru parametrii a si b, intrucat aceasta deschide perspective analizei statistice, analizei economice, prognozei vanzarilor. Pentru a realize astfel de obiective, am fi interesati in obtinerea unor astfel de estimari care sa conduca la:

- obtinerea unui grad de determinare cat mai mare. Asadar, nivelul coeficientului sa fie maxim.

- abaterile dintre valorile empirice privind variabila-efect y si valorile aceleiasi variabile, dar obtinute pe baza modelului si pozitionate exact pe dreapta sa fie cat mai mici. Asadar, minimi sau am putea avea in vedere - minima;

- estimatiile obtinute pentru parametrii sa fie cat mai precise, sa tinda spre adevaratele valori ale parametrilor pe masura ce esantionul creste ca numar de cazuri, sa se abata doar intamplator (si nu sistematic in plus sau sistematic in minus) de la adevaratele valori ale parametrilor. Asadar, estimatiile sa fie eficiente, consistente, nedeplasate.

Dintre metodele de estimare, cele care indeplinesc aceste conditii sunt: metoda verosimilitatii maxime (MVM), metoda celor mai mici patrate (MCMMP), metoda bayesiana. Daca mai avem in vedere si conditia:

- costul sau efortul aplicarii metodei de estimare sa fie cat mai mic (asadar, un criteriu pur economic), atunci metoda celor mai mici patrate pare a fi cea mai apropiata de un astfel de deziderat.

Inainte de a trece la prezentarea si aplicarea MCMMP sa clarificam unele notiuni privind datele si solutiile privind parametrii:

- denumim valori/ niveluri empirice ale variabilei y sau x acele marimi numerice care sunt obtinute din statistici. Astel de valori sunt notate cu respectiv iar pe graphic apar sub forma de puncte de coordonate .

- denumim valori/ niveluri ajustate sau teoretice, acele valori care urmeaza sa fie generate de model. Astfel de valori sunt notate cu . Ele urmeaza sa fie obtinute dupa estimarea parametrilor, iar pe grafic pot sa apara sub forma de cerculete insirate pe dreapta;

- denumim valori adevarate ale parametrilor acele solutii la care se ajunge daca am cunoaste toate valorile pe care variabilele y si x le-au inregistrat. Notam astfel de valori cu a, b iar cu N numarul total de cazuri;

- denimim valori estimate ale parametrilor acele solutii care rezulta in urma utilizarii datelor pe care variabilel le-au inregistrat intr-un esantion de cazuri. Notam astfel de solutii cu iar cu n numarul de cazuri incluse in esantion secvente de date. De mentionat ca in marea majoritate a aplicatiilor se lucreaza cu esantioane asa incat obtinem, fecvent, estimatii. Doar in sfera teoriei si la valorile adevarate ale parametrilor.

Metoda celor mai mici patrate considera abaterea drept element-cheie. Ridicarea la patrat a unei astfel de abateri urmata de insumarea patratelor abaterilor conduce la o suma S. Conditia este ca estimatiile sa fie de o asemenea marime incat suma S sa fie minima.

Asadar,

minima (4

Intrucat , rescriem expresia (4) astfel:

minima (5

Corespunzator teoremei lui Fermat se ajunge la un puct extrem in situatia in care derivata este egala cu zero. Existenta unui numar de doua necunoscute () presupune egalarea cu zero a derivatelor partiale pentru expresia (5) in raport cu fiecare dintre necunoscute.

Ne amintim calculul derivatei pentru o expresie oarecare - conduce la .

In cazul nostru, u=z-a-bx. Asadar, rezulta

(6

(7

Cele doui egalitati la care am ajuns pot fi exprimate, in urma inmultirii, introducerii operatorului de insumare si trecerii cunoscutelor in partea dreapta a egalitatilor, astfel:

(8

.

A rezultat asfel forma standard a ecuatiilor normale. Sistemul este format din 2 ecuatii cu 2 necunoscute, ceea ce face posibila obtinerea solutiilor prin una dintre metodele cunoscute. Solutiile conduc la realizarea unui extrem si anume un extrem minim.

(9

Formula (9) rezulta impartind termenii egalitaatii (8) la n.

(10

Formula rezulta tinand seama de faptul ca iar din (9) . Inlocuim in dupa ce scadem media () din fiecare termen in paranteza rotunda. Obtinem:

(11

Egalam cu zero derivata in raport cu singura necunoscuta , (12

Interpretarea parametrilor estimati

- indica cu cate unitati naturale (in care este exprimat y) se modifica variabula-efect (creste pentru , scade pentru ) daca factorul x creste cu unu (adica cu o unitate naturala in care este exprimat x).

Din perspectiva reprezentarii grafice a functiei liniare (fig. 1), indica panta.

- nu are interpretare economica si ramane cu semnificatia sa cunoscuta de ordonata la origine.

3. Precizari de natura teoretica privind analiza de regresie si modalitatea de estimare a parametrilor

Particularitatea proceselor din economie de a include o partiala incertitudine in manifestare, se constata si in abordarile cauzale, in sensul ca pentru un nivel oarecare al factorului, cosntatam, in mod frecvent, o diversitate de valori privind efectul declansat. Acest aspect poate fi constatat fie pentru mai multe cazuri in care factorul, desi constatat ca nivel, genereaza efecte diferite, fie in situatiile in care analizam mai multe esantioane in cadrul carora, desi un anumit nivel al factorului poate fi identic de la ub esantion la altul, totusi raspunsul este rareori acelasi.

Relatia de dependenta dintre doua variabile apare mult mai evidenta daca avem in vedere, pentru fiecare nivel al factorului, media raspunsurilor. Asadar, media conditionata este pusa in corespondenta cu nivelul .

(13

In situatia in care datele se refera la intreaga populatie, depsebim o functie de regresie a populatiei (FRP), y=a+bx+u. Mediile conditionate ale efectelor, generate de fiecare nivel x al factorului, pot fi reprezentate grafic. Constatari precum: valorile efectelor descriu o repartitie normala in jurul fiecarei medii conditionate; mediile se "insira" pe o dreapta pentru valori in crestere (fig. 2), sugereaza faptul ca ne aflam "umbrela" repartitiei normale, pe de o parte, iar forma liniara a functiei este mai indicata, pe de alta parte.

(14

f()

x

Fig. 2

Coeficineti notati a,b reprezinta, in cazul determinarii lor, valorile adevarate ale parametrilor. Diferemtele (abaterile) dintre valori si media lor reprezinta, figurativ, abaterea aleatoare (), urmare a factorilor accidentali, aleatori, necunoscuti

(15

Daca trecem media in dreapta egalitatii (15, rezulta:

(16

Daca avem in vedere relatia (14), ajungem la egalitatea

(17

Aceasta reprezinta functia de regresie a populatiei (FRP).

In practica rareori se apeleaza la toate cazurile care formeaza populatia, intrucat aceasta varianta de lucru, chiar daca ar fi posibila, implica eforturi deosebite si timp indelungat de culegere a datelor. Este de preferabile alegerea datelor unui esantion.

Pe baza datelor unui esantion putem obtine doar estimari ale parametrilor (notate ), estimari ale mediei conditionate (), estimari ale abaterii () care apar in functia stochastica a esantionului (F.S.E.)

(19

De indata ce obtinem valori estimate pentru constantele functiei stochastice a esantionului, ni se deschid perspective in directii precum:

Cuantificarea rolului variabilei factoriale (x) asupra variabilei-efect, exprimata de nivelul ;

Obtinerea de valori ajustate ale nivelurilor variabilei-efect ( ), adica valori y_i datorate exclusiv influentei factorului considerat determinant, toate celelalte influente perturbatoare fiind "retezate". In subsidiar calculul abaterilor sub forma de resturi date de diferentele este util intrucat analiza unei astfel de serii de valori reziduale (u_i) poate conduce la aprecieri interesante privind calitatea modelului;

Determinarea unor previziuni privind evolutia variabilei-efect () in conditiile in care nivelul viitor al factorului este unul previzibil (prin alte metode) sau preconizat a se realiza (printr-o decizie guvernamentala, urmarea evolutiei naturale etc.) iar schimbari majore in relatia dintre x si y nu se intrevad in viitor.

Astfel de perspective, de interes deosebit pentru analiza si prognoza in economie justifica importanta atribuita estimarii in econometrie dar si interesul acordat verificarii modului in care au fost obtinute estimarile, calitatile acestora si, in general, aprecierea performantelor modelului.

4. Estimarea sub forma de intervale de incredere

Estimatiile parametrilor rezultate pe baza formulelor (9) respectiv (10) sunt punctiforme. Aratam insa ca in situatia in care am utiliza date pentru diferite esantioane de volum n, ne-am putea astepta sa obtinem valori diferite atat pentru , cat si pentru . Doar media estimarilor obtinute, de exemplu, pentru , ne-ar apropia de adevarata valoare b. Afirmam, de asemenea, ca ne situam "sub umbrela" repartitiei normale atat in ceea ce priveste variabila reziduala (u), cat si in ce priveste valorile estimate (, de exemplu) sau eroarea de sondaj.

Pentru a aprecia "virtutile" repartitiei normale, dar si pentru a intelege modul cum este abordata problema intervalului de incredere, reamintim regula celor 3. Conform acestei reguli cunoscute in statistica, pentru o variabila oarecare w, care urmeaza o distributie normala, ne asteptam ca 68,2% dintre valorile acestei variabile sa se situeze intre limitele - si ; 95,44% sa se situeze intre si , iar 99,74% sa se situeze intre si . In cazul in care urmarim sa stabilim intervalul de incredere pentru estimatia care urmeaza, de asemenea o repartitie normala, de medie M()=b, am putea enunta "obiectivul" astfel: ne propunem stabilirea unui interval in cadrul caruia sa se situeze 95% dintre valori. Limitele, conform regulii celor 3 vor fi si , iar k nu va fi nici 2, nici 3, ci o valoare "k" pe care urmeaza sa o stabilim corespunzator P'0,95. in acest scop, ne "adresam" distributiei normale reduse (standard) unde, pentru gasim un nivel al variabilei normal distribuite z, definita intr-o varianta adimensionala, perfect comparabila, astfel:

, respectiv, pentru , .

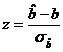Asadar, am stabilit o exprimare comuna a estimatiei si variabilei standardizate z in sensul ca ~ (20

Intrucat, de regula, esantionul /segmentul de date este mic (n<30), este preferata variabila "t" (distributia Student) in loc de variabila z. dar "t" in tabelul repartitiei Student este redat in raport cu dar si in raport cu numarul gradelor de libertate (n-2 parametri), notate g.l.

Asadar ~ (21

Daca nivelul de incredere dorit este de 95 , atunci , iar limitele intervalului rezulta din egalitatea

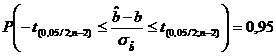(22

Limitele se refera la intervalul in care se va situa "necunoscuta" "b". Solutia inegalitatii 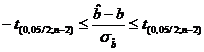, (23

in cazul in care intereseaza limitele intre care se "incadreaza" "b", este data de dubla inegalitate:

(24

Deosebim in stanga limita inferioara de incredere ("lower confidence limit"), iar in dreapta limita superioara ("upper confidence limit"). Intre aceste 2 limite se situeaza nivelul parametrului b in 95 din cazuri.

Pentru exemplificarea bazata pe datele din tabelul 1 am obtinut . Intervalul de incredere in care se situeaza parametrul b (valoare adevarata) daca 16-2 grade de libertate (corespunzator ); , rezulta astfel

Intre 4,4706 si 5,4144 se situeaza nivelul parametrului b cu P

Similar poate fi stabilit intervalul de incredere pentru valorile ajustate (). Avem in vedere, in acest sens, ca depinde si de (intr-adevar ) iar urmeaza o repartitie normala ceea ce face ca aceeasi calitate sa se extinda si asupra ajustarilor ().

Ca urmare, urmand o logica similara precum in cazul estimatiei , rezulta:

(25

Asadar, cu o probabilitate de o marime rezonabila (pentru , probabilitatea este de 0,95) valorile empirice se situeaza intre limitele .

Pozitionarea valorii adevarate a parametrului (24), ca si a valorii empirice (25) aminteste de raspunsul propus de Blaise Pascal la intrebarea "Ce este omul Nimic in raport cu infinitul, totul in raport cu neantul, un lucru de mijloc intre nimic si tot".

5. Proprietatile estimatorilor metodei celor mai mici patrate

Abordarea modalitatii de obtinere a estimatiilor si prin utilizarea metodei celor mai mici patrate din perspectiva calitatii acestora de a "reflecta" (aproxima) suficient de precis valorile adevarate a,b presupune:

acceptarea ideii de a putea obtine estimatii pentru mai multe esantioane de marime identica sau de marime din ce in ce mai mare;

mentinerea, in cazul tuturor esantioanelor, a acelorasi niveluri pentru variabila cauzala   -x;

posibilitatea de a utiliza si alte metode de estimare decat MCMMP;

"prezenta" valorii adaugate a parametrului, fie si in postura de baza de comparare (un fel de valoare-ideal) pentru estimatia obtinuta in diverse conditii de natura metodologica. Daca avem in vedere indeosebi  estimatorul din reprezentarea , atunci , in cazul existentei mai multor esantioane de marime n, obtinem mai multe estimatii a caror repartitie ne asteptam sa "deconspire" valoarea adevarata b. aceasta, prin "aglomerarea" estimatiilor in jurul unei valori centrale (punctul de frecventa maxima-modulul). Exemplificarea unei astfel de situatii este redata in tabelul

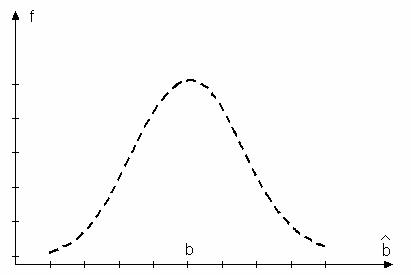
Fig. 3

Tabelul 2

O astfel de situatie in care estimatiile rezultate din diverse esantioane se situeaza fie sub, fie peste valoarea adevarata (intamplator poate coincide cu aceasta) fara preferinte pentru una din cele 2 pozitionari, corespunzator unei repartitii normale, face posibila aprecierea nivelului valorii adevarate a parametrului (b) prin calculul mediei

(26

In exemplul inscris in fig. 3 .

Inexistenta unei distorsiuni in comportamentul estimatiei (in sensul de a inregistra valori predominant superioare valorii adevarate sau predominant inferioare acesteia) confirma relatia 26 si indreptateste etichetarea estimatorului MCMMP ca fiind nedeplasat.

In situatia in care se constata (sau se poate argumenta) ca pe masura ce esantionul creste ("n" devine tot mai mare) estimatia se apropie de valoarea adevarata b, se apreciaza ca esantionul este consistent.

Concret, daca in urma aplicarii MCMMP obtinem, prelucrand datele unui esantion de

n=18 cazuri, =1,17;

n=30 cazuri, =1,6;

n=40 cazuri, =1,53;

n=60 cazuri, =1,49, in situatia in care adevarata valoare a parametrului este b=1,5, afirmam ca estimatorul MCMMP este consistent.

Asadar, la limita, estimatia tinde spre valoarea adevarata, ceea ce poate fi redat astfel:

, (27

unde numar arbitrar oricat de mic

Daca estimatorul MCMMP este nedeplasat si, in plus, estimatiile rezultate in diferite esantioane de volum n prezinta o imprastiere (exprimata de dispersie) mai redusa decat cea care se constata in cazul estimatiilor rezultate din aplicarea altor metode de estimare, se considera ca estimatorul MCMMP este eficient (eficace, precis).

Sa exemplificam o astfel de situatie avand in vedere estimatii pentru parametrul b obtinute prin 2 metode aplicate unui numar de 4 esantioane de volum n

Estimatorul MCMMP este mai precis intrucat dispersia () este mult mai mica fata de ceea ce a rezultat in urma aplicarii celeilalte metode. Intr-adevar 0,085<0,49 si aceasta in conditiile in care calitatea de nedeplasat este specifica ambilor estimatori (mediile estimatiilor fiind identice). Estimatorul MCMMP fiind mai precis (mai putin imprastiat) este eficient in comparatie cu ceea ce rezulta din aplicarea celeilalte metode.

Cele trei calitati atribuite estimatiei obtinute prin MCMMP au fost doar prezentate, dar ele pot fi si argumentate. In cele ce urmeaza, ne referim la argumentarea calitatii de a fi nedeplasat precum si la proprietatea estimatorului MCMMP de a fi cel mai bun estimator liniar nedeplasat ("best linear estimator"-BLUE).

Corespunzator MCMMP, estimatia rezulta astfel (vezi 10): . Daca tinem seama de o proprietate a mediei aritmetice conform careia , precum si de faptul ca ponderea 

exprimata de raportul conduce la egalitatile , si , atunci relatia de estimare a parametrului b (10) poate fi redata astfel:

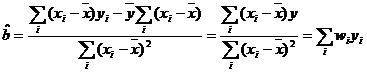(28

Dar asa incat , reprezinta media ponderata a valorilor y_i, ceea ce inseamna ca "produsul" MCMMP este un estimator liniar.

Pentru a arata ca estimatorul are si calitatea de a fi nedeplasat, avem in vedere functia de regresie a populatiei F.R.P. (vezi par. 3) , pe care o introducem in relatia 28 inlocuind variabila y cu expresia sa:

(29

Intrucat am aratat ca iar , relatia 29 devine

  (30

iar redarea in medie conduce la

(31

intrucat M(u)

Asadar, M()=b (32

ceea ce confirma calitatea estimatorului MCMMP de a fi nedeplasat. In ce priveste imprastierea estimatiilor in jurul mediei lor M() (cazul mai multor esantioane), aceasta este redata numeric de dispersie

  (32a

Teorema Gauss - Markov (vezi cap. XVI) arata ca estimatorul MCMMP este de dispersie minima in clasa estimatorilor liniari nedeplasati sau, altfel spus, este cel mai bun (in sens de precis) estimator liniar nedeplasat (BLUE).

Propunem cateva exemplificari care redau la modul figurat calitatile mentionate pentru estimatori:

casierita care "aproximeaza" restul ce ti se cuvine mereu in favoarea ei ca si colega pozitionata in banca in dreapta ta, dar care mereu are ceva de intrebat pe colegul din dreapta ei - ambele au un comportament "deplasat", nicidecum aleatoriu;

conturul unei maini inarmate, care apare tot mai evident intre crengi, pe masura ce fotografia este marita pana la supradimensionare - are ceva din calitatea de "consistent" in planul reprezentarii vizuale ("Blow-up"- film englezesc din anii '70);

rezultatul tragerii la tinta in cazul a 2 tragatori pot fi identice in ce priveste media abaterilor pozitive si negative  fata de centru, dar pot sa difere foarte mult ca precizie (al 2-lea tragator a inregistrat abateri de +3 cm si -1 cm, fata de primul care a inregistrat abaterile +20 cm; -18 cm, ceea ce conduce la medii identice dar, in ce priveste precizia, altfel spus eficienta, aceasta este mult mai mare in cazul primului tragator.

6 Alte metode de estimare

Intre metodele de estimare MCMMP se particularizeaza prin: frecventa utilizarii (cel putin in econometrie), existenta unui numar relativ mare de variante (varianta obisnuita - OLS, variantele in 2 respectiv 3 stadii, varianta ponderata etc.), "atractia" pe care o exercita asupra economistilor. Exista insa si alte metode - la unele ne referim, pe scurt, in cele ce urmeaza (metoda verosimilitatii maxime, metoda bayesiana, metoda punctelor perechi), iar la altele in capitolele urmatoare.

Metoda verosimilitatii maxime (MVM)

Recunoscuta drept un procedeu de estimare dintre cele mai performante, MVM urmareste obtinerea unor astfel de estimatii pentru parametrii incat probabilitatea reproducerii valorilor (datelor) esantionului, folosind estimatiile, sa fie maxima.

Altfel spus, se urmareste obtinerea acelor solutii (pentru parametri) pentru care functia de verosimilitate corespunzatoare, rezultata din repetate sondaje, atinge valoarea sa maxima. Functia de verosimilitate se refera la probabilitatea simultana ce realizare a valorilor privite ca functie de unul sau mai multi parametri. In cazul modelului unifactorial, probabilitatea simultana reprezentata de densitatea de repartitie a valorilor , date fiind constantele a,b,, este reprezentata de

(33

intrucat independenta "extragerilor" implica produsul probabilitatilor. Daca avem in vedere repartitia normala a valorilor y_ij in cazul fiecarui x_i, existenta mai multor esantioane este avuta in vedere de medie M(y /x)=a+bx ;i de dispersie independent[ de x, atunci densitatea de repartitie a valorilor este reprezentata de functia de verosimilitate

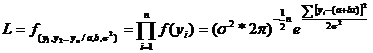(34

In continuare, se urmareste estimarea valorilor a,b, car conduce la maximizarea probabilitatii de reproducere a datelor esantionului ().

Aceasta presupune maximizarea functiei de verosimilitate (34). Se pune, asadar, problema obtinerii unui extrem al unei functii (este preferata relatiei 34, reprezentarea in forma logaritmata , ceea ce se rezolva prin egalarea cu zero a derivatelor partiale in raport cu fiecare dintre cele 3 necunoscute.

(36

(37

.

Ecuatiile la care se ajunge sunt identice cu cele rezultate in cazul MCMMP pentru a si b (vezi 6 - 7) la care se adauga relatia de estimare a necunoscutei (35)

(35

Metoda bayesiana de estimare

Metoda bazata pe analiza bayesiana are in vedere atat datele esantionului (privind ) cat si informatiainformatiile apriori cunoscute privind parametrii (din surse precum teoria economica sau cercetari anterioare). La acestea se adauga, in vederea estimarii, si o functie a pierderii (costului, riscului) datorata abaterilor valorilor estimate de la cele adevarate.

Estimatiile punctiforme rezulta prin introducerea in calcule a ambelor categorii de informatii:

informatii apriorice care conduc la probabilitati apriorice, P(b/I₀);

informatii bazate pe sondaj - carora le este specifica o functie de verosimilitate (P(y/b

Ambele tipuri de informatii conduc la obtinerea asa-numitelor probabilitati revizuite (P(b/y,I₀)).

Introducerea in calcule a functiei pierderi este motivata de considerentul ca abaterea estimatiei de la valoare adevarata provoaca o pierdere (un cost, un risc) proportionala cu marimea abaterii (in valoare absoluta).

Metoda punctelor pereche

In vederea estimarii (aproximarii ar fi mai corect) parametrilor functiei liniare sunt strict necesare doua perechi de valori (existand 2 parametri) alese in zone distincte si, pe cat posibil neafectate de abateri accidentale semnificative.

In cazul in care functia este neliniara(de exemplu, un polinom de gradul 2) alegem un numar de perechi de valori egal cu numarul necunoscutelor (parametrilor). Pentru o cat mai buna aproximare a constantelor modelului se recomanda extrageri de perechi de valori din zone caracteristice relatiei dintre variabile. Astfel, pentru cazul liniar se recomanda perechile de la inceputul, respectiv sfarsitul seriei de date; pentru polinomul de gradul 2, alegem perechi de valori aflate la inceputul seriei, la mijlocul acesteia si in zona finala etc. Sistemul de ecuatii la care se ajunge permite obtinerea solutiilor.